Skoči na vsebino

Podrobneje o zankah

Razvrščanje obratov zank med niti

Dosedaj smo ves čas predpostavljali, da so posamezni obrati vzporedenih zank računsko enako zahtevni. Za učinkovito delovanje programa je torej zadoščalo, da je število obratov enakomerno razporejeno med niti (do razlike za 1 obrat, če število obratov ni deljivo s številom niti).

A posamezni obrati zanke pogosto zahtevajo različno mnogo računskega časa, ki ga je za povrh vsega še težko predvideti v času pisanja programa. Čas izvajanja posameznega obrata je na primer lahko močno odvisen od vhodnih podatkov.

Za prilagajanje razvrščanja obratov zanke vsakokratnim potrebam orodje OpenMP omogoča, da programer z ustreznim dopolnilom ukaza za vzporedenje zanke določi tudi način razvrščanja obratov zanke posameznim nitim:

  • Dopolnilo schedule(static) določa, da se obrate zanke vnaprej enakomerno razdeli med niti: interval obratov se razdeli na podintervale, od katerih gre po en na vsako nit.

  • Dopolnilo schedule(static,n) določa, da se obrate zanke najprej razdeli v skupine po n obratov, te skupine pa se potem ciklično razdeli med niti.

  • Dopolnilo schedule(dynamic,n) določa, da se obrate zanke najprej razdeli v skupine po n obratov, nato pa se jih med izvajanjem dodeljuje prostim nitim - ko nit obdela en skupino n obratov, prevzame naslednjo..

  • Dopolnilo schedule(runtime) določa, da se razvrščanje določi s spremenljivko OMP_SCHEDULE (njeno vrednost nastavimo na primer na eno od gornjih treh možnosti).

Vse to si oglejmo na primeru. V programu schedule-1.c je razvrščanje namenoma nastavljeno na runtime, da lahko uporabljamo spremenljivko OMP_SCHEDULE v ukazni vrstici:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <omp.h>

int main (int argc, char *argv[])
{
  int n; sscanf (argv[1], "%d", &n);

  #pragma omp parallel for schedule(runtime)
    for (int i = 1; i <= n; i++) {
      int s = (i < 4 ? i + 1 : 1);
      printf ("%d:i=%d:s=%d\n", omp_get_thread_num (), i, s);
      sleep (s);
    }
  printf ("\n");

  return 0;
}

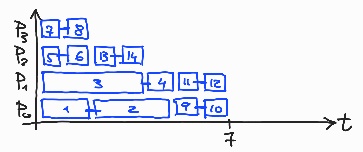
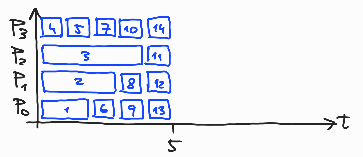
Če poženemo program schedule-1.c s štirimi nitmi in 14 obrati zanke, se glede na izbiro razvrščanja obrati po nitih razporedijo tako, kot je prikazano na slikah 12-16.

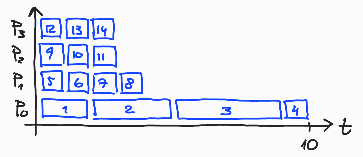
Slika 12: Dodeljevanje 14 obratov zanke med 4 niti: schedule(static).

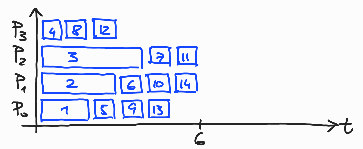
Slika 13: Dodeljevanje 14 obratov zanke med 4 niti: schedule(static,1).

Slika 14: Dodeljevanje 14 obratov zanke med 4 niti: schedule(static,2).

Slika 15: Dodeljevanje 14 obratov zanke med 4 niti: schedule(dynamic,1).

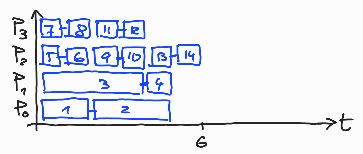
Slika 16: Dodeljevanje 14 obratov zanke med 4 niti: schedule(dynamic,2).

Projekt

Tabelirajte Fibonaccijevo zaporedje 1,1,2,3,5,8,... na intervalu od 1 do n. Izpis je lahko v poljubnem vrstnem redu. Za izračun Fibonaccijevega zaporedja pa uporabitev naivni rekurzivni postopek (brez hranjenja vmesnih rezultatov in podobnih optimizacij), ki se za posamezno število z intervala od 1 do n v celoti izvede v eni sami niti. Izmerite, kako sprememba razvrščanja obratov po nitih vpliva na čas računanja. Za merjenje časa lahko uporabite funkcijo omp_get_wtime.

Združevanje rezultatov obratov zank

Le redko lahko program razdelimo na posamezne obrate zank, ki potem tečejo povsem neodvisno. Prenašanje podatkov iz enega obrata v drugega je možno preko globalnih spremenljivk, paziti pa moramo, da ne pride do nekonsistentnosti podatkov ali izgube (delnih) rezultatov. To sicer lahko pogosto rešimo z atomarnimi operacijami in kritičnimi sekcijami.

Vrnimo se še enkrat k problemu seštevanja števil od 1 do n. Sedaj že vemo, da če to izvedemo z zanko kot v programu error-2.c, tvegamo izgubo kakšnega delnega rezultata prištevanja podobno kot v programu error-1.c.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
#include <stdio.h>

int main (int argc, char *argv[]) {
  int max; sscanf (argv[1], "%d", &max);
  int sum = 0;
  #pragma omp parallel for
    for (int i = 1; i <= max; i++)
      sum = sum + i;
  printf ("%d\n", sum);
  return 0;
}

Tudi v programu error-2.c bi lahko težavo odpravili z uporabo atomarne operacije ali kritične sekcije, a ker je računanje globalne vsote tako pogost vzorec v programih, zanj obstaja v orodju OpenMP posebna rešitev: redukcija. Ta je prikazana v programu ints-sum-1.c: z dopolnilom reduction(+:sum) dosežemo,

  • da se sicer skupna spremenljivka sum v nitih obnaša kot zasebna,
  • ob koncu pa se vse zasebne spremenljivke sum posameznih niti seštejejo v skupno spremenljivko sum.

Namesto seštevanja lahko seveda uporabimo tudi druge operatorje.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
#include <stdio.h>

int main (int argc, char *argv[]) {
  int max; sscanf (argv[1], "%d", &max);
  int sum = 0;
  #pragma omp parallel for reduction(+:sum)
    for (int i = 1; i <= max; i++)
      sum = sum + i;
  printf ("%d\n", sum);
  return 0;
}

Vaja

Na primeru seštevanja števil izmerite, kako hitre so atomarne operacije, kritične sekcije in redukcije. Za merjenje časa lahko uporabite funkcijo omp_get_wtime.

Projekt

Število pi lahko izračunamo tako, da naključno streljamo v kvadrad s stranico dolžine 1 in izračunamo razmerje med streli, ki so znotraj četrtine kroga s polmerom 1, ki ima središče v spodnjem levem vozlišču kvadrata. Napišite program, ki po tej metodi izračuna število pi in pri tem enakomerno obremeni vse strojne niti programa.