Introduction to Matrix Multiplication with OpenMP

Authors: Matic Brank

This course will guide you through implementing matrix multiplication using OpenMP parallelization. We'll start with a basic implementation and gradually optimize it.

Prerequisites

Basic C/C++ programming knowledge
Understanding of basic matrix multiplication
GCC compiler with OpenMP support

Natural Parallelism and Matrix Multiplication

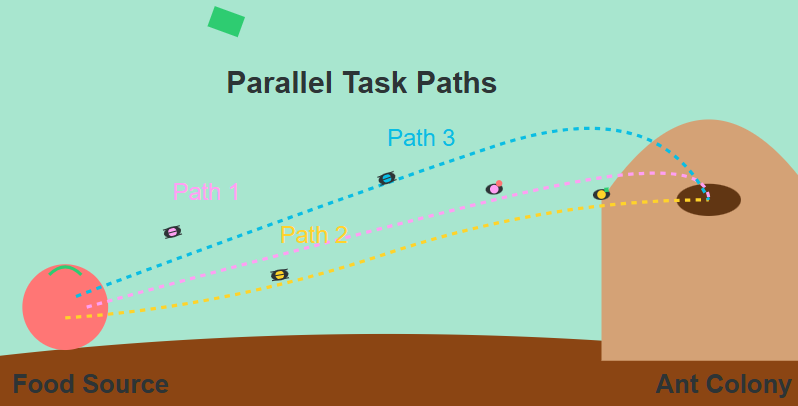
In nature, we can observe a fascinating example of parallel processing in how ant colonies gather food. When ants discover a food source, they don't work in isolation - instead, they divide into multiple groups, with each group taking responsibility for a specific area or path. These groups work simultaneously, efficiently moving food pieces back to their nest. Each ant doesn't need to know about the entire operation; it just needs to focus on its assigned task while contributing to the colony's overall goal. This natural division of labor allows ant colonies to accomplish complex tasks much faster than if a single ant tried to do everything sequentially.

Natural Parallelism {:style="width:linewidth"}

*Natural Parallelism *

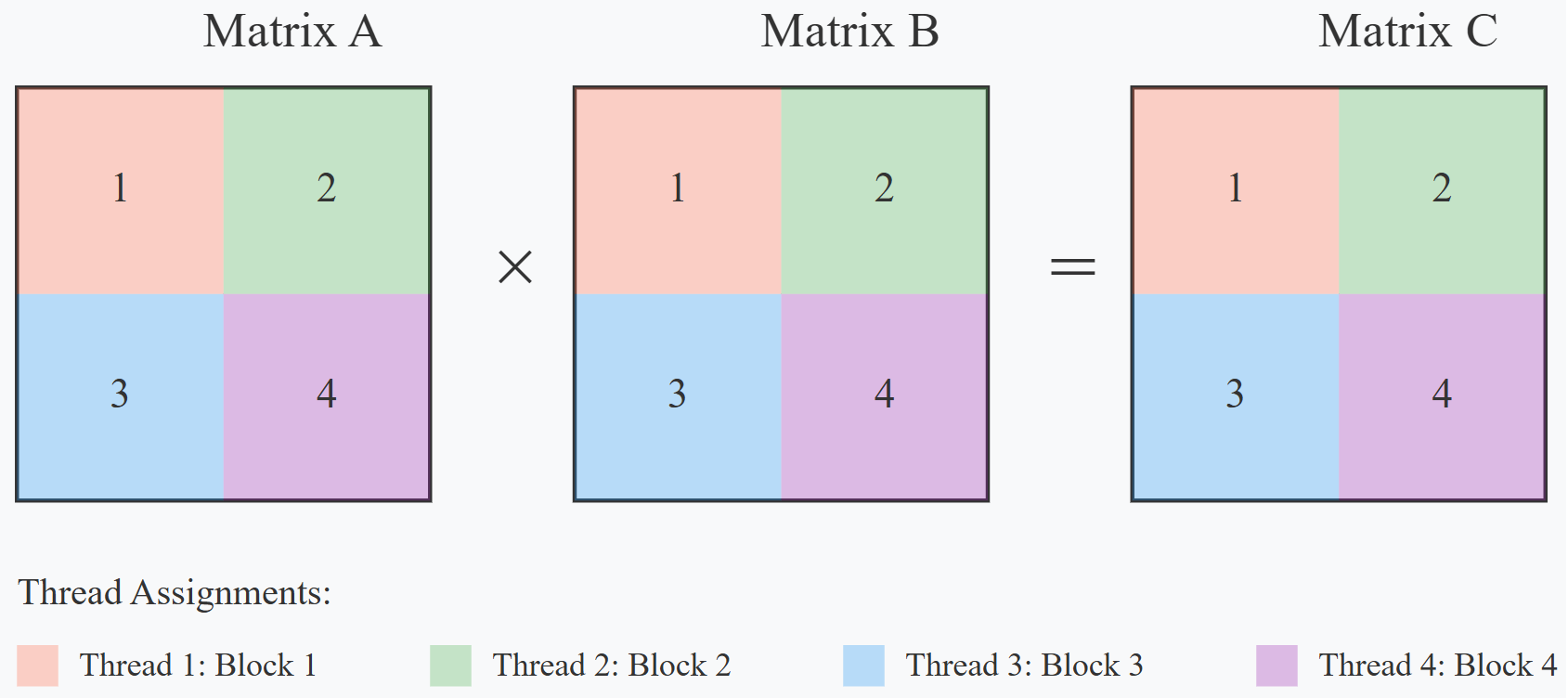
Similarly, when we perform matrix multiplication in computing, we face a task that can be naturally divided into independent pieces that can be processed simultaneously. Just as ant colonies speed up their food gathering by having multiple groups work in parallel, we can speed up matrix multiplication by dividing the work among multiple CPU cores using OpenMP. Each core, like an individual ant group, can focus on computing its assigned portion of the final matrix, working independently yet contributing to the overall result. This parallel approach can significantly reduce computation time, especially for large matrices, making it essential for modern high-performance computing applications in fields like scientific simulation, machine learning, and computer graphics.

Matrix Multiplication {:style="width:linewidth"}

*Matrix Multiplication*

This course will guide you through implementing matrix multiplication using OpenMP parallelization. We'll start with a basic implementation and gradually optimize it.

Part 1: Introduction to OpenMP

What is OpenMP?

Standard programming model for shared memory parallel programming
Portable across all shared-memory architectures
It allows incremental parallelization
Compiler based extensions to existing programming languages
Fortran and C/C++ binding

Ownership and timeline

Ownership - OpenMP ARB (Architecture review board) - Its mission is to standardize directive-based multi-language high-level parallelism that is performant, productive and portable - Jointly defined by a group of major computer hardware and software vendors and major parallel computing user facilities (such as AMD, Intel, IBM, HP, Fujitsu, Microsoft,…)

Release history - 1997 OpenMP - Fortran 1.0 - 1998 OpenMP - C/C++ 1.0 - 1999 OpenMP - Fortran 1.1 - 2000 OpenMP - Fortran 2.0 - 2002 OpenMP - C/C++ 2.0 - 2005 OpenMP 2.5 - 2008 OpenMP 3.0 - 2013 OpenMP 4.0 - 2018 OpenMP 5.0 stable release - 2020 OpenMP 5.1 release

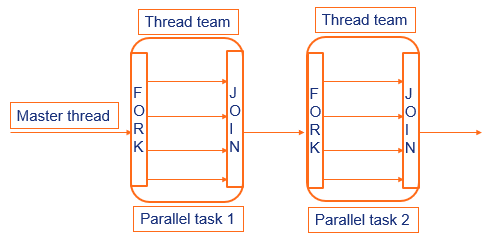
OpenMP – Main terminology - OpenMP thread: a running process specified by OpenMP - Thread team: a set of threads which cooperate on a task - Master thread: Main thread which coordinates the parallel jobs - Thread safety: This term refers to correct execution of multiple threads - OpenMP directive: OpenMP line of code for compilers with OpenMP - Construct: an OpenMP executable directive - Clause: controls the scoping of the variables during execution

OpenMP – Execution model

Thread based parallelism
Compiler directive based parallelism
Explicit parallelism
Fork-Join model
Dynamic Threads
Nested parallelism

OpenMP – Execution model {:style="width:linewidth"}

*OpenMP – Execution model*

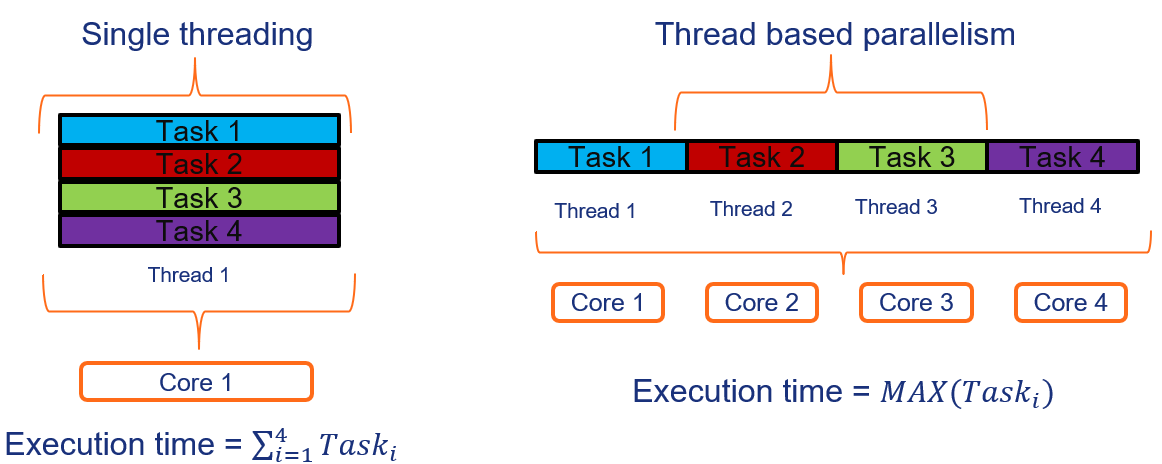
Thread based parallelism

Thread based parallelism {:style="width:linewidth"}

*Thread based parallelism*

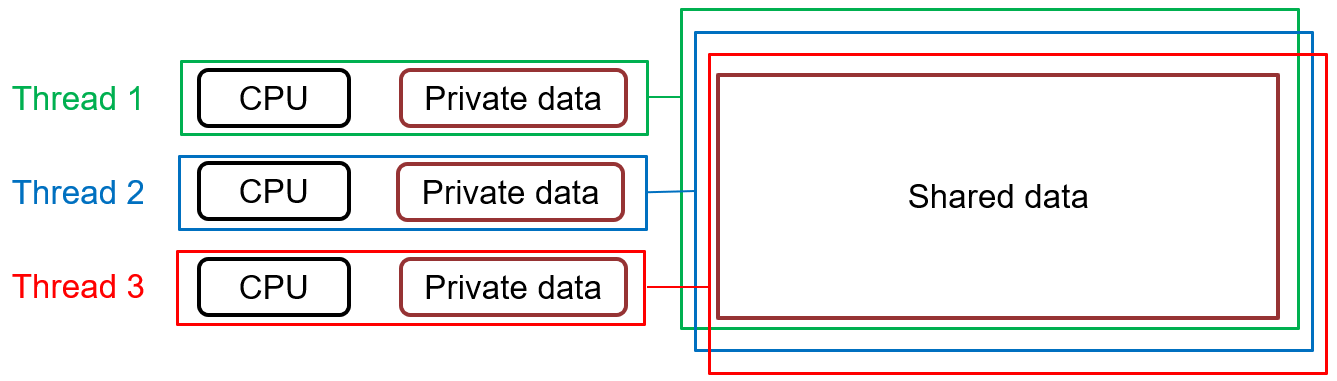
OpenMP memory model

All threads have access to the same memory
Threads can share data with other threads, but also have private data
Threads can be synchronized
Threads cache their data

OpenMP memory model {:style="width:linewidth"}

*OpenMP memory model*

Part 2: Basic Matrix Multiplication

Let's start with a simple sequential implementation:

// Function performs matrix multiplication C = A × B
// Parameters:
//   A: Input matrix A (N×N)
//   B: Input matrix B (N×N)
//   C: Output matrix C (N×N)
//   N: Size of the matrices (N×N)
void matrix_multiply_basic(double* A, double* B, double* C, int N) {
    // Loop through each row of matrix A
    for (int i = 0; i < N; i++) {
        // Loop through each column of matrix B
        for (int j = 0; j < N; j++) {
            // Initialize accumulator for dot product
            double sum = 0.0;

            // Compute dot product of row i from A and column j from B
            for (int k = 0; k < N; k++) {
                // A[i * N + k]: Access element at row i, column k in matrix A
                // B[k * N + j]: Access element at row k, column j in matrix B
                // For example, if N=3, accessing A[1,2] would be A[1 * 3 + 2]
                sum += A[i * N + k] * B[k * N + j];
            }

            // Store the result in matrix C at position (i,j)
            // C[i,j] contains dot product of row i from A and column j from B
            C[i * N + j] = sum;
        }
    }
}

Additional explanation of the indexing: - The matrices are stored in row-major order (standard C/C++ layout) - For a matrix element at row r and column c, the memory index is r * N + c - For example, in a 3×3 matrix, element [1,2] would be at index 1 * 3 + 2 = 5:

[0 1 2] // Indices: 0,1,2

[3 4 5] // Indices: 3,4,5

[6 7 8] // Indices: 6,7,8

Part 3: Adding OpenMP Parallelization

Now, let's add basic OpenMP parallelization:

// Include OpenMP header for parallel processing directives
#include <omp.h>

void matrix_multiply_parallel_v1(double* A, double* B, double* C, int N) {
    // OpenMP directive to parallelize the following nested loops
    // #pragma omp parallel for: Creates a team of threads that divide the iterations
    // collapse(2): Combines the first two nested loops (i and j) into a single loop
    // This creates a larger parallel workload (N*N iterations instead of just N)
    // For example, with N=1000, instead of 1000 parallel tasks, we get 1000*1000 tasks
    #pragma omp parallel for collapse(2)
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            // sum is private to each thread by default
            // Each thread gets its own copy of sum variable
            double sum = 0.0;

            // This innermost loop (k) is not parallelized
            // It runs sequentially within each thread
            // Each thread computes one complete element of the result matrix C
            for (int k = 0; k < N; k++) {
                sum += A[i * N + k] * B[k * N + j];
            }

            // Each thread writes its result to a different location in C
            // No synchronization needed as there are no write conflicts
            // (different threads write to different elements of C)
            C[i * N + j] = sum;
        }
    }
}

Key parallelization concepts: 1. #pragma omp parallel for: - Creates multiple threads - Divides loop iterations among threads - Each thread executes its assigned iterations independently 2. collapse(2): - Combines two nested loops into a single parallel loop - Increases parallel granularity - Better load balancing across threads - For example, with N=1000: - Without collapse: 1000 parallel tasks - With collapse: 1000*1000 = 1 million parallel tasks 3. Data sharing: - Arrays A, B, C are shared by all threads (read/write access) - Loop variables (i, j, k) are private to each thread - sum variable is automatically private to each thread 4. Thread safety: - Each thread writes to different elements of C - No need for critical sections or atomic operations - No race conditions as there's no overlap in output locations

Part 4: Cache Optimization

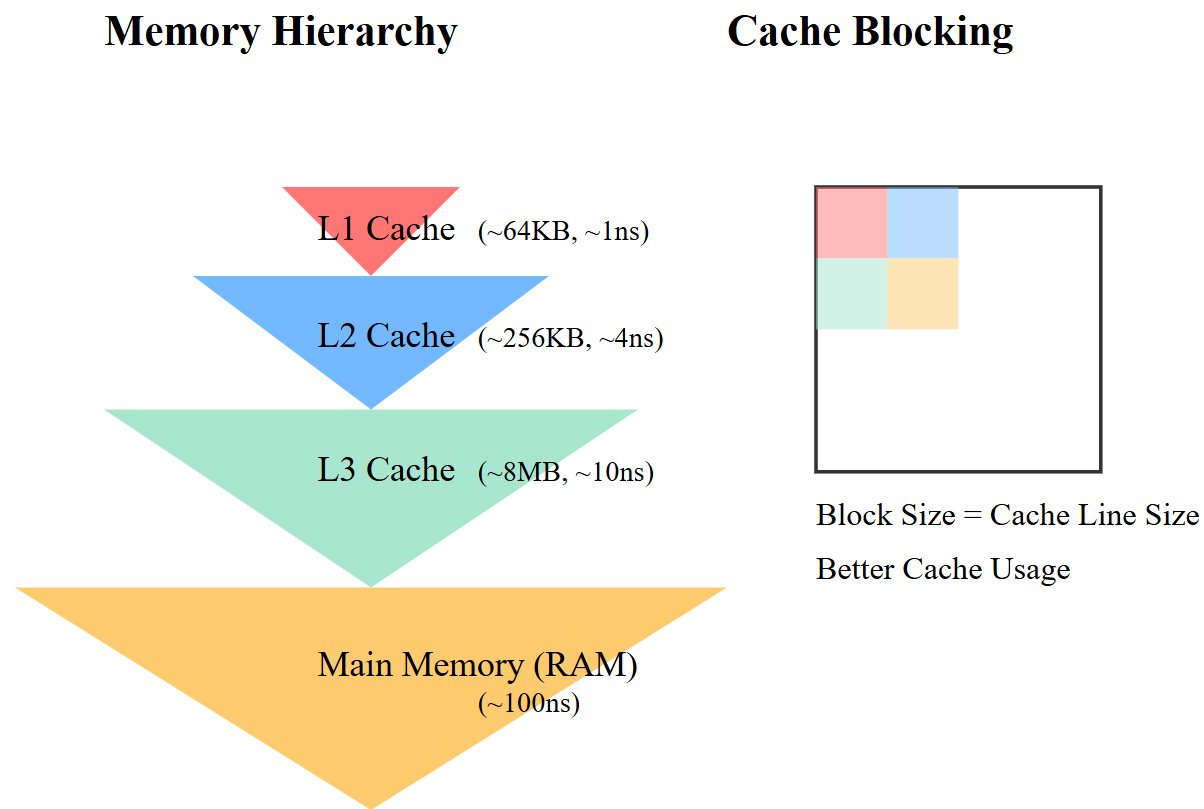
Cache optimization refers to techniques that improve how efficiently a program uses the CPU's cache memory. The cache is a small, very fast memory that sits between the main memory (RAM) and the CPU. It temporarily stores frequently accessed data to reduce the time spent waiting for data from slower main memory.

Cache Optimization {:style="width:linewidth"}

*Cache Optimization*

Key aspects of cache optimization: 1. Cache Hierarchy: - L1 Cache: Smallest (~64KB) but fastest (~1ns access) - L2 Cache: Larger but slower than L1 - L3 Cache: Even larger but slower than L2 - Main Memory (RAM): Largest but slowest (~100ns access) 2. Cache Blocking (Tiling): For matrix multiplication, we use cache blocking by:

    const int BLOCK_SIZE = 32;  // Choose size to fit in L1 cache
    for (int ii = 0; ii < N; ii += BLOCK_SIZE) {
        for (int jj = 0; jj < N; jj += BLOCK_SIZE) {
        // Process small blocks that fit in cache

Benefits of Cache Optimization:
- Reduces memory access time
- Improves data locality
- Reduces cache misses
- Better performance
Common Techniques:
- Block size selection based on cache size
- Data alignment
- Sequential access patterns
- Minimizing cache line thrashing

Let's improve cache utilization with blocking:

// Blocked (tiled) matrix multiplication implementation that optimizes cache usage
// By dividing matrices into smaller blocks that fit in cache
void matrix_multiply_blocked(double* A, double* B, double* C, int N) {
    // BLOCK_SIZE should be chosen based on cache size and architecture
    // For example: L1 cache = 32KB, double = 8 bytes
    // Block should fit 3 matrices: A, B, C blocks
    // 32 * 32 * 8 bytes * 3 = 24KB (fits in L1 cache)
    const int BLOCK_SIZE = 32;

    // Parallelize the two outermost loops that iterate over blocks
    // This assigns different blocks to different threads
    #pragma omp parallel for collapse(2)
    // Outer loops iterate over blocks (ii, jj, kk are block indices)
    for (int ii = 0; ii < N; ii += BLOCK_SIZE) {
        for (int jj = 0; jj < N; jj += BLOCK_SIZE) {
            // kk loop iterates over blocks needed for current block multiplication
            for (int kk = 0; kk < N; kk += BLOCK_SIZE) {
                // Inner loops iterate within each block
                // min() handles edge cases where N is not multiple of BLOCK_SIZE
                for (int i = ii; i < min(ii + BLOCK_SIZE, N); i++) {
                    for (int j = jj; j < min(jj + BLOCK_SIZE, N); j++) {
                        // Initialize sum with current value of C
                        // This allows for accumulation across kk blocks
                        double sum = C[i * N + j];

                        // Innermost loop operates on a block of data that should
                        // now be in cache due to spatial locality
                        for (int k = kk; k < min(kk + BLOCK_SIZE, N); k++) {
                            sum += A[i * N + k] * B[k * N + j];
                        }

                        // Store result back to C matrix
                        C[i * N + j] = sum;
                    }
                }
            }
        }
    }
}

Cache Optimization Details: 1. Block Size Selection:

    const int BLOCK_SIZE = 32;
- Chosen to fit in L1 cache
- Need to store three blocks: one each from A, B, and C
- Calculate size: 32 × 32 × 8 bytes × 3 = 24KB
- Typical L1 cache is 32KB-64KB
- Powers of 2 work well with cache line sizes

Memory Access Pattern:
```
for (int ii = 0; ii < N; ii += BLOCK_SIZE)
for (int jj = 0; jj < N; jj += BLOCK_SIZE)
for (int kk = 0; kk < N; kk += BLOCK_SIZE)
```
- Divides matrices into smaller blocks
- Each block fits in cache
- Reduces cache misses significantly
- Improves spatial and temporal locality
- Cache Benefits:
- Spatial Locality:
  - Accessing consecutive elements within a block
  - Utilizes full cache lines
  - Reduces memory bandwidth requirements
- Temporal Locality:
  - Reuses data while it's still in cache
  - Block of matrix A is reused for each column in block of B
  - Block of B is reused for each row in block of A
- Edge Cases:
  
  i < min(ii + BLOCK_SIZE, N) - Handles matrices where N is not multiple of BLOCK_SIZE - Prevents out-of-bounds access - Maintains correctness at matrix edges 5. Performance Considerations: - Each thread works on independent blocks - No false sharing between threads - Cache lines aren't shared between cores - Reduces cache coherency traffic

Part 5: Advanced Optimizations

Here's the optimized matrix multiplication code with detailed comments explaining all the advanced optimization techniques:

// Highly optimized matrix multiplication combining multiple optimization techniques:
// - Cache blocking
// - Thread-local storage
// - SIMD vectorization
// - Dynamic scheduling
// - Memory alignment
void matrix_multiply_optimized(double* A, double* B, double* C, int N) {
    // Block size chosen to fit in L1 cache and align with CPU vector units
    // 32 x 32 doubles = 8KB, allows for good cache utilization
    const int BLOCK_SIZE = 32;

    // Create parallel region - all threads execute this block
    #pragma omp parallel
    {
        // Allocate thread-local storage aligned to 64-byte boundary
        // - 64 bytes matches typical cache line size
        // - Alignment enables efficient SIMD operations
        // - Thread-local storage prevents false sharing between threads
        double* temp_C = (double*)aligned_alloc(64, BLOCK_SIZE * BLOCK_SIZE * sizeof(double));

        // Parallelize block computation with dynamic scheduling
        // - collapse(2) combines loops for better load balancing
        // - schedule(dynamic) helps with uneven workload distribution
        // - Good for heterogeneous systems or when blocks take different times
        #pragma omp for collapse(2) schedule(dynamic)
        for (int ii = 0; ii < N; ii += BLOCK_SIZE) {
            for (int jj = 0; jj < N; jj += BLOCK_SIZE) {
                // Initialize temporary block to zeros
                // Using smaller BLOCK_SIZE indices for better cache behavior
                for (int i = 0; i < BLOCK_SIZE; i++) {
                    for (int j = 0; j < BLOCK_SIZE; j++) {
                        temp_C[i * BLOCK_SIZE + j] = 0.0;
                    }
                }

                // Main computation loop over blocks
                for (int kk = 0; kk < N; kk += BLOCK_SIZE) {
                    // Process each row within current block
                    for (int i = 0; i < BLOCK_SIZE && (ii + i) < N; i++) {
                        // Process each element in the current row of block A
                        for (int k = 0; k < BLOCK_SIZE && (kk + k) < N; k++) {
                            // Cache A's element for reuse in inner loop
                            // Reduces memory access in innermost loop
                            double a_val = A[(ii + i) * N + (kk + k)];

                            // Enable SIMD vectorization for innermost loop
                            // Modern CPUs can process 4-8 doubles simultaneously
                            #pragma omp simd
                            for (int j = 0; j < BLOCK_SIZE && (jj + j) < N; j++) {
                                // Accumulate product in thread-local storage
                                // - Better cache utilization
                                // - Avoids false sharing
                                // - Enables vectorization
                                temp_C[i * BLOCK_SIZE + j] += 
                                    a_val * B[(kk + k) * N + (jj + j)];
                            }
                        }
                    }
                }

                // Copy computed block back to global result matrix
                // Boundary checks prevent buffer overruns
                for (int i = 0; i < BLOCK_SIZE && (ii + i) < N; i++) {
                    for (int j = 0; j < BLOCK_SIZE && (jj + j) < N; j++) {
                        C[(ii + i) * N + (jj + j)] = temp_C[i * BLOCK_SIZE + j];
                    }
                }
            }
        }

        // Free thread-local storage to prevent memory leaks
        free(temp_C);
    }
}

Key Optimization Details: 1. Memory Alignment and Thread-Local Storage:

    double* temp_C = (double*)aligned_alloc(64, BLOCK_SIZE * BLOCK_SIZE * sizeof(double));
- 64-byte alignment matches cache line size
- Prevents false sharing between threads
- Enables efficient SIMD operations
- Each thread has its own temporary storage

Dynamic Scheduling:
```
#pragma omp for collapse(2) schedule(dynamic)
```
- Better load balancing
- Handles non-uniform workloads
- Good for heterogeneous systems
- Reduces thread idle time
- SIMD Vectorization:
  
  pragma omp simd
  
  for (int j = 0; j < BLOCK_SIZE && (jj + j) < N; j++) - Enables CPU vector instructions - Processes multiple elements simultaneously - Can achieve 4-8x speedup on modern CPUs - Automatic vectorization of innermost loop 4. Cache Optimization:
  
  double a_val = A[(ii + i) * N + (kk + k)]; - Caches frequently used values - Reduces memory access - Better temporal locality - More efficient use of cache hierarchy 5. Boundary Handling:
  
  for (int i = 0; i < BLOCK_SIZE && (ii + i) < N; i++) - Safe handling of matrix edges - No buffer overruns - Works with any matrix size - Clean handling of non-multiple sizes

Part 6: Performance Analysis

To measure performance, compile with:

gcc -O3 -fopenmp -march=native your_program.c -o gemm

Benchmark your implementation:

// Get the starting time using OpenMP's high-precision timer
// omp_get_wtime() returns a double-precision value in seconds
// It's more precise than time() or clock() and works well with OpenMP
double start = omp_get_wtime();

// Execute the optimized matrix multiplication function
// This is the section we're measuring
matrix_multiply_optimized(A, B, C, N);

// Get the ending time after computation is complete
double end = omp_get_wtime();

// Calculate and print the elapsed time
// Subtracting start from end gives us the duration in seconds
// %f format specifier prints as floating point number
printf("Time: %f seconds\n", end - start);

Additional notes on timing measurement: 1. omp_get_wtime(): - Returns wall-clock time (real-world elapsed time) - Has high precision (typically microsecond or better) - Is thread-safe and OpenMP-aware - Measures time across all threads 2. Why not use other timing methods: - clock(): Only measures CPU time, not wall time - time(): Only second-level precision - gettimeofday(): Not as portable across systems

Common performance metrics: 1. GFLOPS (Giga Floating Point Operations Per Second) 2. Memory bandwidth utilization 3. Cache miss rates (use tools like perf)

Practice Exercises

Basic Implementation:
- Implement the basic parallel version
- Experiment with different thread counts
- Measure speedup vs sequential version
Cache Optimization:
- Implement blocked version
- Experiment with different block sizes
- Measure impact on performance
Advanced Features:
- Add SIMD vectorization
- Implement thread-local storage
- Compare performance with different scheduling strategies

Tips for Best Performance

Choose appropriate block sizes based on your CPU's cache size
Use aligned memory allocation for better vectorization
Experiment with thread counts and scheduling policies
Profile your code to identify bottlenecks
Consider CPU architecture-specific optimizations

Remember that optimal performance depends on: - Matrix size - CPU architecture - Memory hierarchy - Number of available cores - Thread affinity settings