Skip to content

Skalarni produkt vektorjev1

Poskusimo se sedaj poigrati z malo bolj zanimivim problemom. Tokrat bomo namesto seštevanja vektorjev sprogramirali skalarni produkt dveh vektorjev - istoležne elemente najprej zmnožimo med seboj, nato pa zmnožke seštejemo.

Naiven pristop

Prva implementacija skalarnega produkta bo na las podobna seštevanju vektorjev. Ideja je, da niti na GPE delajo produkte med istoležnimi elementi vektorjev, medtem ko gostitelj sešteje vse delne produkte. Ščepec za produkte istoležnih elementov vektorjev je: 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
__kernel void DotProd_naive(__global float* vecA,
                __global float* vecB,
                __global float* vecC,
                int iNumElements) {

    // get index into global data array
    int iGID = get_global_id(0);
    int iGS = get_global_size(0);

    while (iGID < iNumElements) {
        //add the vector elements
        vecC[iGID] = vecA[iGID] * vecB[iGID];
        iGID = iGID + iGS;
    }

}

Gostitelj mora po končanem izvajanju ščepca prebrati vektor produktov iz naprave ter v zanki sešteti vse njegove elemente:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
    / Synchronous/blocking read of results
    status = clEnqueueReadBuffer(
                                cmdQueue,
                                vecC_d,
                                CL_TRUE,
                                0,
                                datasize,
                                vecC_h,
                                0,
                                NULL,
                                NULL);
    clerr_chk(status);


    // Block until all previously queued OpenCL commands in a command-queue
    // are issued to the associated device and have completed
    clFinish(cmdQueue);

    // sum of partial products:
    float result = 0.0;
    for (int i=0; i<iNumElements; i++) {
        result += vecC_h[i];
    }

Celotno kodo iz tega poglavja najdete v mapi 05-dot-product-naive tukaj.

Skalarni produkt z redukcijo in uporabo lokalnega spomina

V zgornjem primeru mora gostitelj sešteti vse delne produkte. Če so vektorji zelo dolgi, bo gostitelj potreboval veliko časa za prenos delnih produktov iz naprave, nato pa delne produkte tudi precej časa sešteval. Zato bomo sadaj predstavili rešitev, s katero bodo niti seštele vse delne produkte. Pri tem bomo spoznali, kako lahko niti uporabljajo lokalni pomnilnik ter kako sodelujejo pri računanju. Računanje skalarnega produkta bo sestavljeno iz treh korakov:

  1. N niti bomo razdelili v G delovnih skupin. Vsaka nit v delovni skupini bo računala delne produkte med istoležnimi elementi vektorjev in jih seštevala v svoj delni produkt, ki ga bo hranila v lokalnem pomnilniku. Ker bomo imeli v delovni skupini L=N/G niti, bomo imeli na koncu tega koraka L delnih produktov shranjenih v lokalnem pomnilniku.
  2. Nato bodo vse niti znotraj ene delovne skupine skupaj sodelovale pri seštevanju L delnih produktov v delovni skupini ter svoj rezultat shranile na predvideno mesto v globalnem pomnilniku naprave. Za G delovnih skupin, bomo imeli na koncu tega koraka G seštevkov delnih produktov v globalnem pomnilniku naprave.
  3. Na gostitelja bomo zdaj prenesli samo G seštevkov iz globalnega pomnilnika naprave in jih tam sešteli. Ker je delovnih skupin G mnogo manj od velikosti vektorjev N, bo gostitelj prenašal bistveno manj podatkov in imel pri seštevanju precej manj dela.

Korak 1: delni produkti v skupini

Spodnja koda prikazuje del ščepca, zadolženega za množenje istoležnih elementov vektorjev ter seštevanje produktov.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
    int myGID = get_global_id(0);
    int myLID = get_local_id(0);
    int myWGID = get_group_id (0);

    __local float vecC_wg[64];

    vecC_wg[myLID] = 0.0;

    while (myGID < iNumElemements) {
        vecC_wg[myLID] += vecA[myGID] * vecB[myGID];
        myGID += get_global_size (0);
    }

    //-- wait at the barrier!
    barrier(CLK_LOCAL_MEM_FENCE);

V našem primeru bomo imeli v eni delovni skupini 64 niti. Najprej v vrstici 5 deklariramo polje, v katerem bo vsaka nit v delovni skupini shranila seštevek svojih produktov:

5
__local float vecC_wg[64];

Z dopolnilom __local določimo, da se polje vecC_wg hrani v lokalnem pomnilniku. Čeprav je ta deklaracija navedena za vsako nit v skupini, bo prevajalnik v lokalnem pomnilniku računske enote ustvaril le eno polje, ki bo skupno vsem nitim v delovni skupini.

Nato v vrstici 7 vsaka nit inicializira svoj element, ki bo hranil njen seštevek delnih produktov.

Vrednost myLID določa indeks niti v delovni skupini. Tako bo vsaka nit inicializirala le element polja, ki pripada njej.

Sedaj v zanki while (vrstice 9 do 12)

 9
10
11
12
    while (myGID < iNumElemements) {
        vecC_wg[myLID] += vecA[myGID] * vecB[myGID];
        myGID += get_global_size (0);
    }

vsaka nit množi istoležne elemente vektorjev, ki ustrezajo njenemu globalnemu indksu ter produkte prišteva v vecC_wg[myLID].

Preden v drugem koraku seštejemo vse elemente polja vecC_wg[myLID], moramo biti prepričani, da so vse niti v skupini zaključile izvajanje zanke while . Pravimo, da se morajo niti počakati pri prepreki (ang. barrier). Prepreke v OpenCL izvedemo s funkcijo barrier(CLK_LOCAL_MEM_FENCE). Funkcija blokira nadaljnje izvajanje programa, dokler je ne pokličejo vse niti v delovni skupini. Z drugimi besedami, vse niti v delovni skupini morajo poklicati funkcijo barrier(CLK_LOCAL_MEM_FENCE) preden lahko katerakoli nit nadaljuje z izvajanjem programa.

Korak 2: vsota delnih produktov v skupini

V drugem koraku moramo sešteti vse elemente polja vecC_wg[myLID]. Naivno bi to rešili tako, da bi samo ena nit v delovni skupini seštela vse te elemente. Vendar obstaja boljša rešitev, ki jo prikazuje spodnja slika:

Redukcija

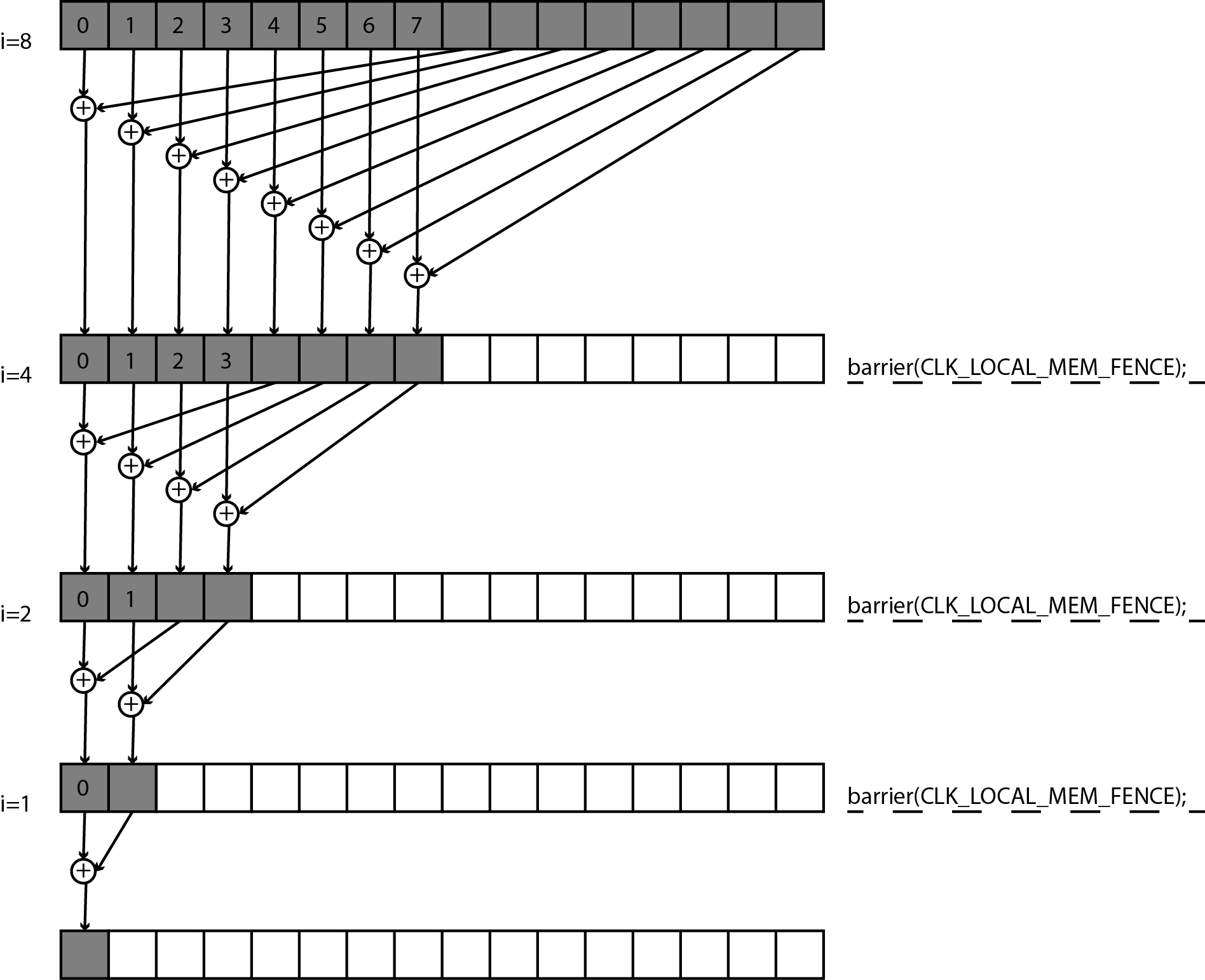
Za seštevanje elementov bomo uporabili postopek, ki mu pravimo redukcija. Predpostavimo, da imamo le 16 elementov, ki jih moramo sešteti ter 16 niti v delovni skupini. V prvem koraku bo vsaka od prvih osmih niti v delovni skupini seštela element z njenim indeksom myLID ter element z indeksom myLID+8 in vsoto zapisala v element z indeksom myLID. Preostalih osem niti v delovni skupini ne bo delalo ničesar. Nato se bodo vse niti počakale pri prepreki. V naslednjem koraku bo le še vsaka od prvih štiri niti seštela element z njenim indeksom myLID ter element z indeksom myLID+4, ostale niti ne bodo seštevale. Preden nadaljujejo z delom, se bodo vse niti spet počakale pred prepreko. Tako bomo nadaljevali postopek dokler ne bo ostala samo ena nit z indeksom 0, ki bo seštela element z indeksom 0 in element z indeksom 1. Postopek pravkar opisane redukcije prikazuje spodnja koda v vrsticah od 24 do 34.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
__kernel void DotProd_reduction (__global float* vecA,
                __global float* vecB,
                __global float* localproducts,
                int iNumElemements) {

    int myGID = get_global_id(0);
    int myLID = get_local_id(0);
    int myWGID = get_group_id (0);

    __local float vecC_wg[64];

    vecC_wg[myLID] = 0.0;

    while (myGID < iNumElemements) {
        vecC_wg[myLID] += vecA[myGID] * vecB[myGID];
        myGID += get_global_size (0);
    }

    //-- wait at the barrier!
    barrier(CLK_LOCAL_MEM_FENCE);

    localproducts[myWGID] = 0.0;

    // Reduction:
    int i = get_local_size (0) / 2;
    while (i != 0) {
        if (myLID < i) {
            //perform the addition:
            vecC_wg[myLID] += vecC_wg[myLID + i];
        }
        i = i/2;
        // wait at the barrier:
        barrier(CLK_LOCAL_MEM_FENCE);
    }

    // only one WI writes the result:
    if (myLID == 0) {
        localproducts[myWGID] = vecC_wg[0];
    }
}

Pozoren bralec bo opazil, da funkcijo barrier(CLK_LOCAL_MEM_FENCE) kličejo vse niti v skupini in ne samo tiste, ki seštevajo. Razlog tiči v tem, da funkcija barrier(CLK_LOCAL_MEM_FENCE) zahteva, da jo izvedejo vse niti v skupini preden bi lahko katerakoli nit nadaljevala z delom. Če bi funkcijo barrier(CLK_LOCAL_MEM_FENCE) naivno postavili v vejitev (stavek if), bi se izvajanje ščepca za vedno ustavilo pri prepreki, saj bi niti, ki pridejo do prepreke, čakale na vse preostale niti v skupini, ki niso izvajale vejitve.

Ob koncu redukcije bo vsota vseh elementov v polju vecC_wg[myLID] zapisana v elementu vecC_wg[0]. Nazadnje bo nit z myLID=0 ta rezultat prepisala v globalni pomnilnik naprave v polje localproducts na mesto z indeksom, ki ustreza indeksu delovne skupine myWGID (vrstice 36 do 39):

36
37
38
39
    // only one WI writes the result:
    if (myLID == 0) {
        localproducts[myWGID] = vecC_wg[0];
    }

Program na gostitelju tokrat zahteva manjše spremembe. Delni rezultati, ki jih bomo prebrali iz naprave, bodo sedaj vsebovani v polju vecC_d, ki bo imelo le toliko elementov, kolikor je delovnih skupin:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
    const size_t szLocalWorkSize = 64;
    const size_t szGlobalWorkSize = 2048;
    int iNumGroups = (int)(szGlobalWorkSize / szLocalWorkSize);

    size_t datasizeC = sizeof(cl_float) * iNumGroups;

    // Use clCreateBuffer() to create a buffer object (d_C)
    // with enough space to hold the output data
    vecC_d = clCreateBuffer(
                             context,
                             CL_MEM_WRITE_ONLY,
                             datasizeC,
                             NULL,
                             &status);
    clerr_chk(status);
V zgornji kodi smo predpostavili, da poženemo le 2048 niti in da ima vsaka delovna skupina 64 niti.

Nazadnje mora gostitelj prebrati delne produkte posameznih delovnih skupin in jih sešteti.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
    // Synchronous/blocking read of results
    status = clEnqueueReadBuffer(
                                cmdQueue,
                                vecC_d,
                                CL_TRUE,
                                0,
                                datasizeC,
                                vecC_h,
                                0,
                                NULL,
                                NULL);
    clerr_chk(status);

    // Block until all previously queued OpenCL commands in a 
    // command-queue are issued to the associated device and have completed
    clFinish(cmdQueue);

    // check the result
    float result = 0.0;
    for (int i=0; i<iNumGroups; i++) {
        result += vecC_h[i];
    }

Celotno kodo iz tega poglavja najdete v mapi 06-dot-product-reduction tukaj.

Merjenje časa izvajanja ščepcev

Čas izvajanja ščepcev na GPE lahko tudi merimo. Za to uporabimo t.i. dogodke (ang. event) - od GPE naprav lahko zahtevamo, da nam sporočajo vse dogodke vezane na ukaze, ki jih pošiljamo po ukaznih vrstah. Dva zanimiva dogodka sta začetek in konec izvajanja ščepca. Za merjenje časa izvajanja ščepca moramo:

  1. pri ustvarjanju ukaznih vrst omogočiti uporabo dogodkov (profiling):
1
2
3
4
5
cmdQueue = clCreateCommandQueue(
    context,
    devices[0],
    CL_QUEUE_PROFILING_ENABLE,  // enable profiling
    &status);
  1. ukaz za zagon ščepca povežemo z dogodkom (zadnji argument):
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
    cl_event event;
    // Launch kernel
    status = clEnqueueNDRangeKernel(
        cmdQueue,
        ckKernel,
        2,
        NULL,
        szGlobalWorkSize,
        szLocalWorkSize,
        0,
        NULL,
        &event);  // link to event
    clerr_chk(status);
  1. po zagonu ščepca čakamo na dogodek:
1
clWaitForEvents(1, &event);
  1. ko prenesemo rezultate iz GPE nazaj na gostitelja, z uporabo OpenCL API funkcije clGetEventProfilingInfo preberemo časa dveh dogodkov CL_PROFILING_COMMAND_START in CL_PROFILING_COMMAND_END ter izračunamo razliko med njima:
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
cl_ulong time_start;
cl_ulong time_end;

clGetEventProfilingInfo(event, 
    CL_PROFILING_COMMAND_START, 
    sizeof(time_start), 
    &time_start, 
    NULL);
clGetEventProfilingInfo(event, 
    CL_PROFILING_COMMAND_END, 
    sizeof(time_end), 
    &time_end, 
    NULL);

double nanoSeconds = time_end-time_start;
printf("Kernel Execution time is: %0.3f milliseconds \n",nanoSeconds / 1000000.0);

Celotno kodo iz tega poglavja najdete v mapi 07-dot-product-profiling tukaj.

  1. © Patricio Bulić, Univerza v Ljubljani, Fakulteta za računalništvo in informatiko. Gradivo je objavljeno pod licenco Creative Commons Priznanje avtorstva-Nekomercialno-Deljenje pod enakimi pogoji 4.0 Mednarodna. ↩