Image processing¹

Edge enhancement is an image processing filter that increases the contrast of edges of an image in an attempt to improve its sharpness. The edge is defined as a significant local change in image intensity. For an ideal edge, the change in intensity occurs in steps of one pixel. Ideal edges are very rare in images, especially if the images are smoothed beforehand to remove noise from them. Changes in intensity, therefore, occur at several consecutive pixels; such an edge is called a ramp.

The edge enhancement filter works by recognizing sharp edges in the image (for example, the edge between the subject and the background) and increasing the contrast of the image in the area immediately around the edge. This makes the edge look more defined. The image below shows an example of highlighting edges:

Input image	Output image

We use a 3x3 discrete Laplace operator for the edge enhancement process. Laplacian is a second-order derivative mask; its usage highlights edges in an image. The important thing is how to apply these filters to an image. First, each image pixel and its eight surrounding pixels in the original image are multiplied by the corresponding values in the Laplace operator. Secondly, products are added together. The sum of products represents a new value of the corresponding pixel in the output image with highlighted edges. We refer to this process as convolution. The figure below shows one step of the convolution with the Laplace operator.

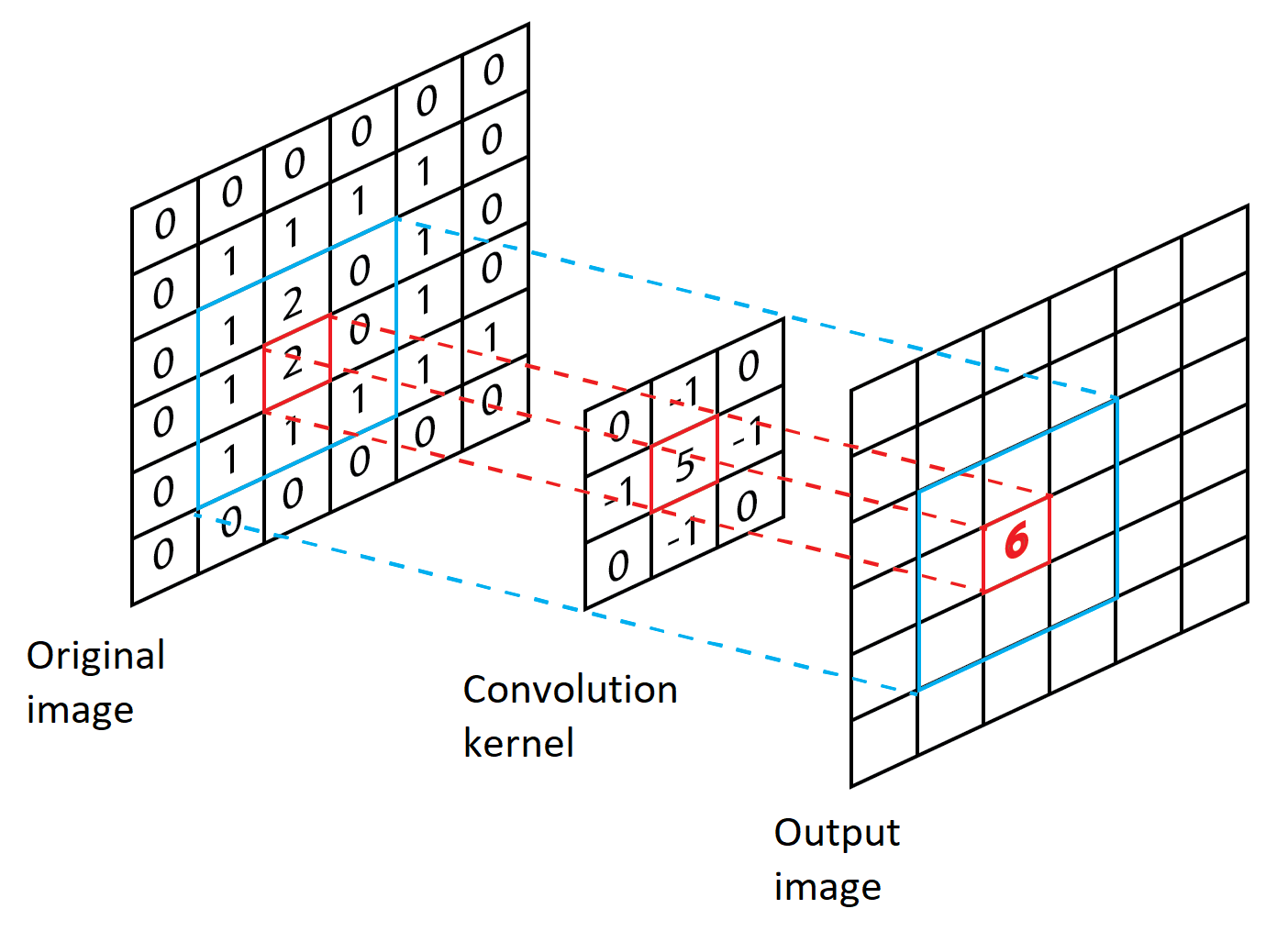
The figure also shows the Laplace operator, which we use to enhance the edges in the figure. For example, we can see how we emphasize the pixel' with a value of 2, which forms an edge with a pixel on its right (value 0). The new value, 6, is obtained by placing the core on the original image, multiplying the identical elements and adding the partial products.

Image manipulation

We will use the public STB library to read images from disk to memory and write them back to disk. The STB library is a collection of single-file header-file libraries for C/C++ in the public domain. The library is quite extensive, but we will only use the stbi_load and stbi_write functions, which are defined in the stb_image.h and stb_image_write.h headers. Instructions for using the functions can be found here.

Images representation in memory

We will first read the images from the files on the disk into memory. Images are stored in memory as an array of pixels. For grayscale images, one pixel is usually represented by eight bits that define the grayscale level (black to white). The image plane of the dimension Width x Height is represented in the memory as a 1D vector of image pixels, where an individual image pixel is accessed as follows: image [Y x Width + X]. Access to each image pixel in a one-channel image is shown in the image below.

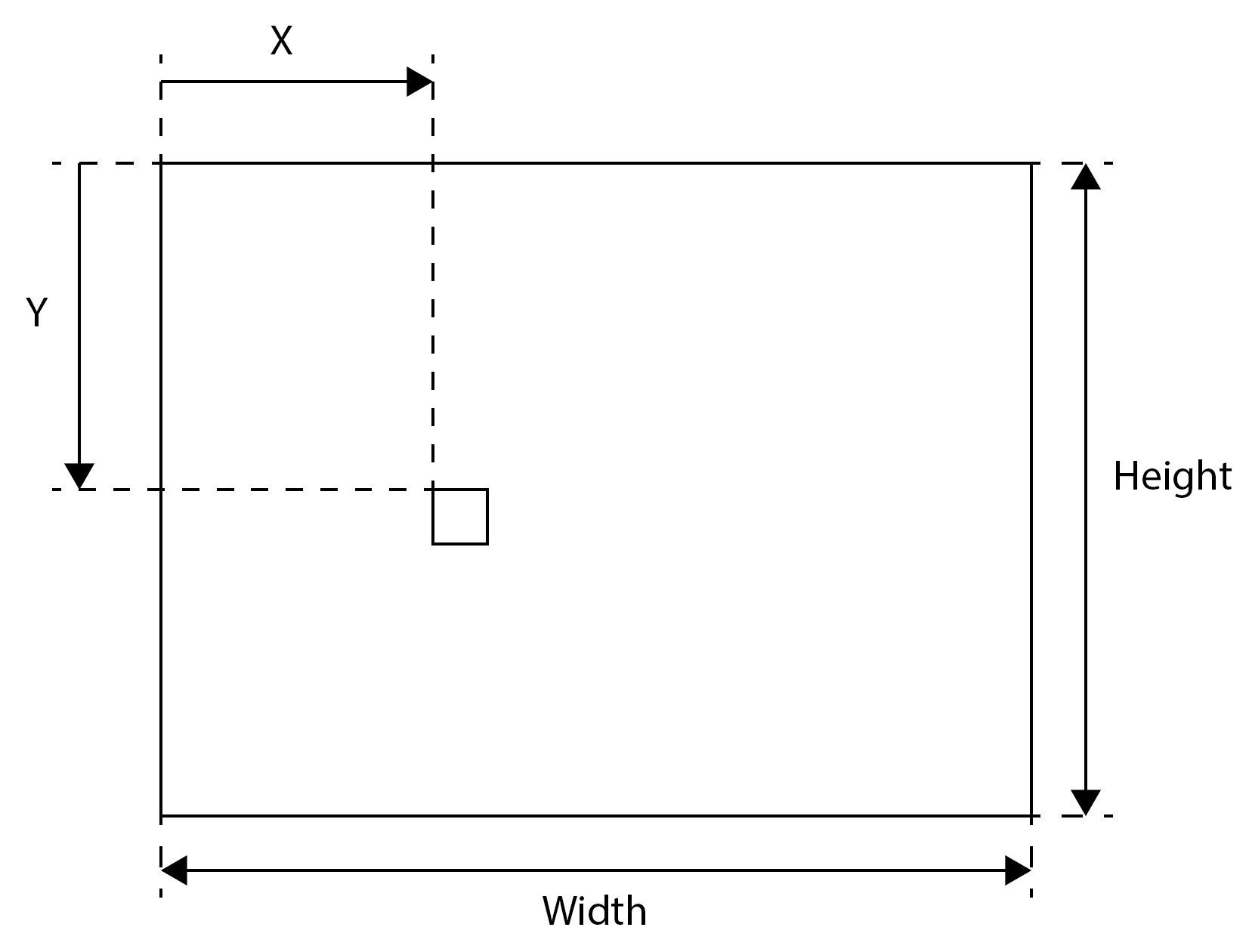
The quantities X (column),Y (row), Width (width) andHeight (height) are expressed in pixels.

For colour images, typically, each pixel is represented by 4 x 8 bits or four bytes. The first three bytes specify the three colour components (RGB, Red, Green, and Blue), while the last byte specifies transparency for specific image formats (such as png). We also say that an image consists of four channels. Each pixel is therefore represented in memory by four values, each value being written with one byte. The four-channel image of the Width x Height dimensions in memory is shown in the image below.

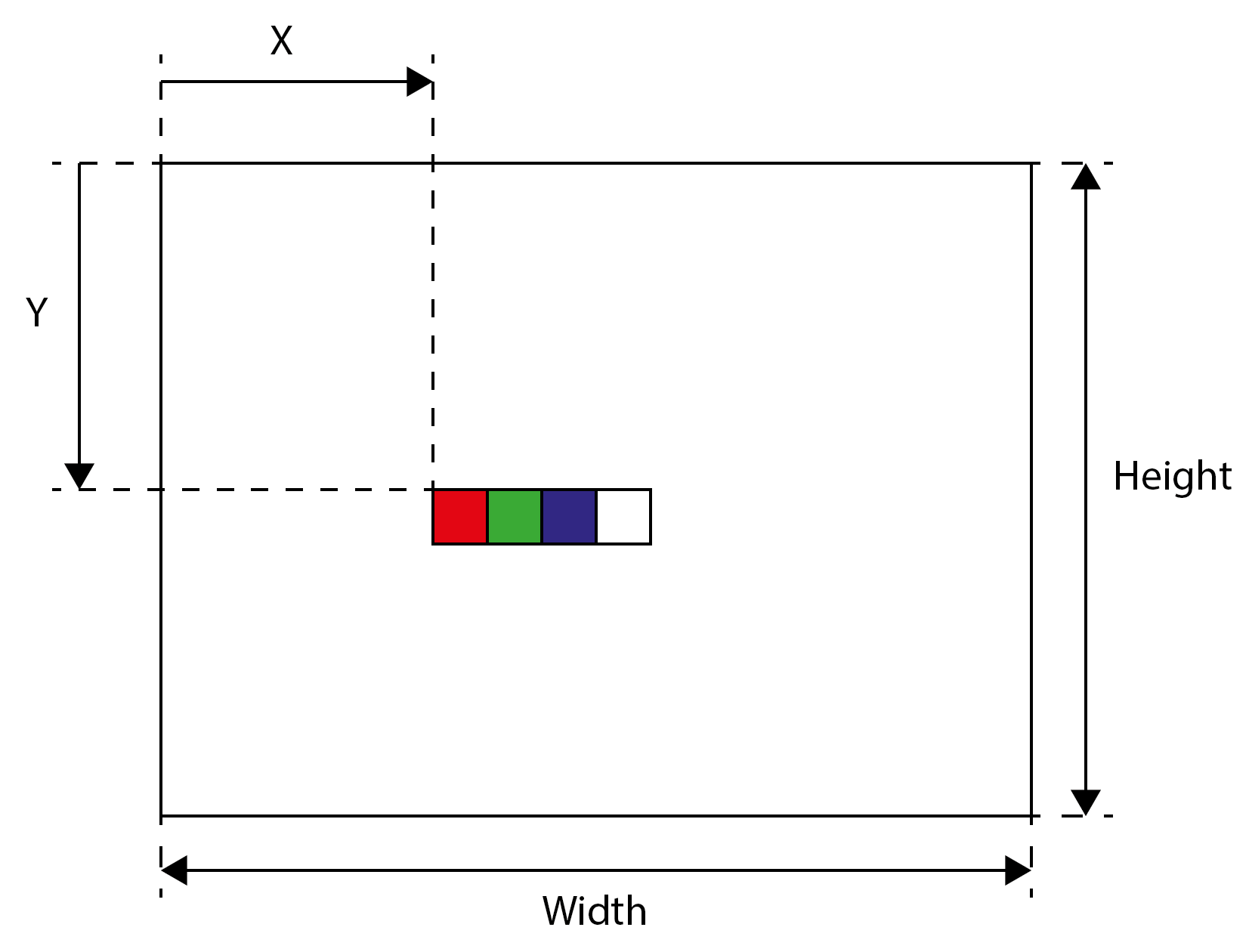
An individual pixel is now accessed as follows:

image [(Y x Width + X) x CPP + channel],

where CPP is the number of channels per pixel and can take values between 1 and 4, whereas channel is a channel index with a value from 0 to 3.

We will limit ourselves to four-channel images and write them to memory with the stbi_load function. In the case of grayscale images (one channel), the last three bytes of the pixel will be unused. At first glance, the solution is wasteful, as grayscale images take up four times memory space as needed. Still, we will have the same code to process all types of images.

Edge enhancement kernel

Each thread will calculate a new value of one pixel in the image. For this purpose, with 3x3 filters, it will have to access eight surrounding pixels of the pixel for which it calculates the new value. However, with the Laplace kernel for edge enhancement, it is sufficient to access only four adjacent pixels at which the kernel has nonzero values. The edge-enhancement sharpen kernel is implemented in the code below.

//***************************************************
// Image sharpening using a 3x3 kernel; Source: https://setosa.io/ev/image-kernels/
//
//      |  0  -1   0 |
// K =  | -1   5  -1 |
//      |  0  -1   0 |
//
//***************************************************

// CUDA kernel for image sharpening. Each thread computes one output pixel
__global__ void sharpen(const unsigned char *imageIn, unsigned char *imageOut, const int width, const int height, const int cpp)
{
    // Get pixel
    int x = blockIdx.x * blockDim.x + threadIdx.x;
    int y = blockIdx.y * blockDim.y + threadIdx.y;

    if (x < width && y < height)
    {
        for (int c = 0; c < cpp; c++)
        {
            unsigned char px01 = getIntensity(imageIn, y - 1, x, c, height, width, cpp);
            unsigned char px10 = getIntensity(imageIn, y, x - 1, c, height, width, cpp);
            unsigned char px11 = getIntensity(imageIn, y, x, c, height, width, cpp);
            unsigned char px12 = getIntensity(imageIn, y, x + 1, c, height, width, cpp);
            unsigned char px21 = getIntensity(imageIn, y + 1, x, c, height, width, cpp);

            short pxOut = (5 * px11 - px01 - px10 - px12 - px21);
            pxOut = MIN(pxOut, 255);
            pxOut = MAX(pxOut, 0);
            imageOut[(y * width + x) * cpp + c] = (unsigned char)pxOut;
        }
    }
}

In the for loop, we walk across all channels. Then, for each channel separately, the thread reads the values ​​of five pixels from the image: the pixel for which it calculates the new value, and its four neighbours (left, right, top and bottom), as required by the Laplace operator. To access the values ​​of individual pixels, we have prepared the getIntensity function:

__device__ inline unsigned char getIntensity(const unsigned char *image, int row, int col,
                                             int channel, int height, int width, int cpp)
{
    if (col < 0 || col >= width)
        return 0;
    if (row < 0 || row >= height)
        return 0;
    return image[(row * width + col) * cpp + channel];
}

Such a kernel is simple, but it has one serious drawback. As we have written many times, access to main memory is always done by all threads from a warp simultaneously and is always 128 bytes long - four bytes per thread. In our case, each thread needs only one of four bytes in one iteration, discarding unnecessary ones! Then in the next iteration, it accesses the same segment in global memory again, even though it accessed this segment in the previous iteration! But what if, during the last iteration, it simply discarded the data it didn't need at the time.

The two-dimensional grid is set up as follows:

    dim3 blockSize(BLOCK_SIZE, BLOCK_SIZE);
    dim3 gridSize(ceil(width / blockSize.x), ceil(height / blockSize.y));

where the value of BLOCK_SIZE is 16. The threads will be grouped in 16 x 16 thread blocks. The total number of threads depends on the size of the input image and must be divisible in both dimensions by the block size, which is 16. Since the dimensions of input images are not necessarily divisible by 16, we should round up the image size so that it is divisible by 16 when determining the number of threads.

The sharpen kernel needs 0.115 milliseconds to process and image of size 2580x1319 pixels on Tesla V100 GPU:

$ srun --partition=gpu --gpus=1 prog helmet_in.png helmet_out.png
Loaded image helmet_in.png of size 2580x1319.
Kernel Execution time is: 0.115 miliseconds

The above code is published in folder 07-image-filter of the workshop's repo.

---

1. © Patricio Bulić, University of Ljubljana, Faculty of Computer and Information Science. The material is published under license CC BY-NC-SA 4.0. ↩