Dot product¹

Let us now take a look at the vector dot product. We will start with the simple version to illustrate the basic memory and thread management features in CUDA. Next, we will recap the usage of grids, thread blocks and threads. Then we will analyze the performance of this simple version and extend it to the version that employs local memory.

Naïve implementation of dot product

The complete program for the naïve version of dot product is:

#include <stdio.h>
#include <stdlib.h>

#include <cuda.h>
#include <cuda_runtime.h>

#include "helper_cuda.h"

// CUDA kernel. Each thread takes care of one element of c
__global__ void dotProduct(const float *a, const float *b, float *c, const int n)
{
    // Get global thread ID
    int tid = blockIdx.x * blockDim.x + threadIdx.x;

    // Make sure we do not go out of bounds
    while (tid < n)
    {
        c[tid] = a[tid] * b[tid];
        tid += gridDim.x * blockDim.x;
    }
}

int main(int argc, char *argv[])
{
    // Size of vectors
    int n = 1024;
    size_t datasize = sizeof(float) * n;

    // Host input vectors
    float *h_a;
    float *h_b;
    // Host output vector
    float *h_c;

    // Device input vectors
    float *d_a;
    float *d_b;
    // Device output vector
    float *d_c;

    // Allocate memory for each vector on host
    h_a = (float *)malloc(datasize);
    h_b = (float *)malloc(datasize);
    h_c = (float *)malloc(datasize);

    // Allocate memory for each vector on GPU
    checkCudaErrors(cudaMalloc(&d_a, datasize));
    checkCudaErrors(cudaMalloc(&d_b, datasize));
    checkCudaErrors(cudaMalloc(&d_c, datasize));

    // Initialize vectors on host
    for (int i = 0; i < n; i++)
    {
        h_a[i] = 1.0;
        h_b[i] = 1.0;
    }

    // Copy host vectors to device
    checkCudaErrors(cudaMemcpy(d_a, h_a, datasize, cudaMemcpyHostToDevice));
    checkCudaErrors(cudaMemcpy(d_b, h_b, datasize, cudaMemcpyHostToDevice));

    dim3 blockSize = 64;
    dim3 gridSize = n / blockSize.x;

    // Execute the kernel
    dotProduct<<<gridSize, blockSize>>>(d_a, d_b, d_c, n);
    getLastCudaError("dotProduct() execution failed\n");

    // Copy array back to host
    checkCudaErrors(cudaMemcpy(h_c, d_c, datasize, cudaMemcpyDeviceToHost));

    // Sum up the products
    float result = 0.0;
    for (int i = 0; i < n; i++)
        result += h_c[i];
    printf("Result = %.2f \n", result);

    // Release device memory
    checkCudaErrors(cudaFree(d_a));
    checkCudaErrors(cudaFree(d_b));
    checkCudaErrors(cudaFree(d_c));

    // Release host memory
    free(h_a);
    free(h_b);
    free(h_c);

    return 0;
}

The computation of a vector dot product consists of two steps. In the first step, the kernel computes the pairwise products. The kernel function for the first step is:

// CUDA kernel. Each thread takes care of one element of c
__global__ void dotProduct(const float *a,
                           const float *b,
                           float *c,
                           const int n)
{
    // Get global thread ID
    int tid = blockIdx.x * blockDim.x + threadIdx.x;

    // Make sure we do not go out of bounds
    while (tid < n)
    {
        c[tid] = a[tid] * b[tid];
        tid += gridDim.x * blockDim.x;
    }
}

First, we multiply the corresponding elements of two input vectors. This is very similar to vector addition but utilizes multiplication instead of addition. Each thread multiplies a pair of corresponding vector elements and then moves on to its next pair. Just like in the addition example, the threads increment their indices by the total number of threads in the grid. In the second step, we sum up all the products. After the kernel has finished execution, the host must read the vector of products from the device and sum up all its elements in a loop:

    // Sum up the products
    float result = 0.0;
    for (int i = 0; i < iNumElements; i++)
        result += h_c[i];
    printf("Result = %.2f \n", result);

Everything else in the host code is the same as in the vector addition program.

The above code is published in folder 04-dot-product-naive of the workshop's repo.

Dot product optimized: usage of shared memory and reduction

The problem with the previous implementation is that the host computes the sum of partial pairwise products. In the case of very long vectors, this would require a significant time.

Therefore, we will present a better solution to sum up partial products. We will learn how threads can use shared memory and cooperate in addition. The calculation of the scalar product will consist of three steps:

N threads will be divided into B thread blocks with L threads per block. Each thread in the block will compute the pairwise products of the vectors and store them into its partial dot product, which will be stored in the shared memory. Since we have L=N/B threads in the block, there will be L partial products stored in the shared memory at the end of this step.
All threads within one block will then cooperate to combine the sum of L partial dot products. One of the threads in the block will store this sum in the device's global memory. For B blocks, we will have B sums in the device's global memory at the end of this step.
We will now transfer only B sums from the device's global memory to the host and sum up them there. Because the number of blocks B is much smaller than the size of the vectors N, the host will have to transfer significantly fewer data from the device. Moreover, the host will have much less work to sum them up into the final dot product.

Step 1: partial dot products in the thread block

The code below shows the kernel part responsible for multiplying the corresponding elements of the vectors and adding the partial products into the array buf.

    // Get global thread ID
    int tid = blockIdx.x * blockDim.x + threadIdx.x;

    __shared__ float buf[BLOCK_SIZE];

    // Initialize shared buffer
    buf[threadIdx.x] = 0;

    __syncthreads();

    // Make sure we do not go out of bounds
    while (tid < iNumElemements)
    {
        buf[threadIdx.x] += a[tid] * b[tid];
        tid += gridDim.x * blockDim.x;
    }

    __syncthreads();

The array buf is kept in shared memory and is of size BLOCK_SIZE. BLOCK_SIZE is equal to the number of threads in the thread block. To allocate local memory, simply use the __shared__ address space qualifier in a variable declaration:

__shared__ float buf[BLOCK_SIZE];

Since the compiler creates a copy of the shared variables for each thread block, we need to allocate enough memory such that each thread in the block has an entry. Now, each thread initializes its entry in the array buf:

 buf[threadIdx.x] = 0;

We need a method to guarantee that all of these writes to the shared array buf complete before any thread tries to read from this buffer. Fortunately, such a method exists:

 __syncthreads();

This call guarantees that every thread in the block has completed instructions before the __syncthreads() and only then allows the hardware to execute the next instruction on any thread. This is known as a barrier. In general, a barrier is a thread synchronization construct that, when used at a point in the code, is called by each and every thread reaching that point, such that no thread makes progress beyond this construct until all threads (of the block) have arrived at this synchronization point. Once all threads have reached the barrier, they can proceed to execute the next instruction. Suppose, for some reason, some threads don't reach the barrier. In that case, the remaining threads which reached the barrier will simply wait forever for the former, and there is a deadlock. CUDA provides barrier synchronization to synchronize the execution of warps within a block. Hence, every warp in a block must wait for all warps of its thread block to arrive at the barrier (call __syncthreads()) before it can proceed to execute the next instruction after the barrier call.

Each thread can now multiply two corresponding elements and sums up the partial products into its entry in the buffer buf:

    // Make sure we do not go out of bounds
    while (tid < iNumElemements)
    {
        buf[threadIdx.x] += a[tid] * b[tid];
        tid += gridDim.x * blockDim.x;
    }

 __syncthreads();

At this point in the algorithm, we need to sum up all the temporary values we’ve placed in the array buf. To do this, we will need some of the threads to read the values that have been stored in the array buf. However, as we mentioned, we need a second barrier that ensures that all threads have finished writing into array buf:

Step 2: Summation reduction

Now that we have guaranteed that our local memory buf has been filled with partial products, we can sum the values in it. We call the general process of taking an input array and performing some computations that produce a smaller array of results a reduction. The naïve way to accomplish this reduction would be to have one thread iterate over the shared memory and calculate a running sum. This would take us time proportional to the length of the array. However, since we have hundreds of threads in the group available to do this work, we can do this reduction in parallel and take the time that is proportional to the logarithm of the length of the array. The following figure shows a summation reduction:

Summation reduction

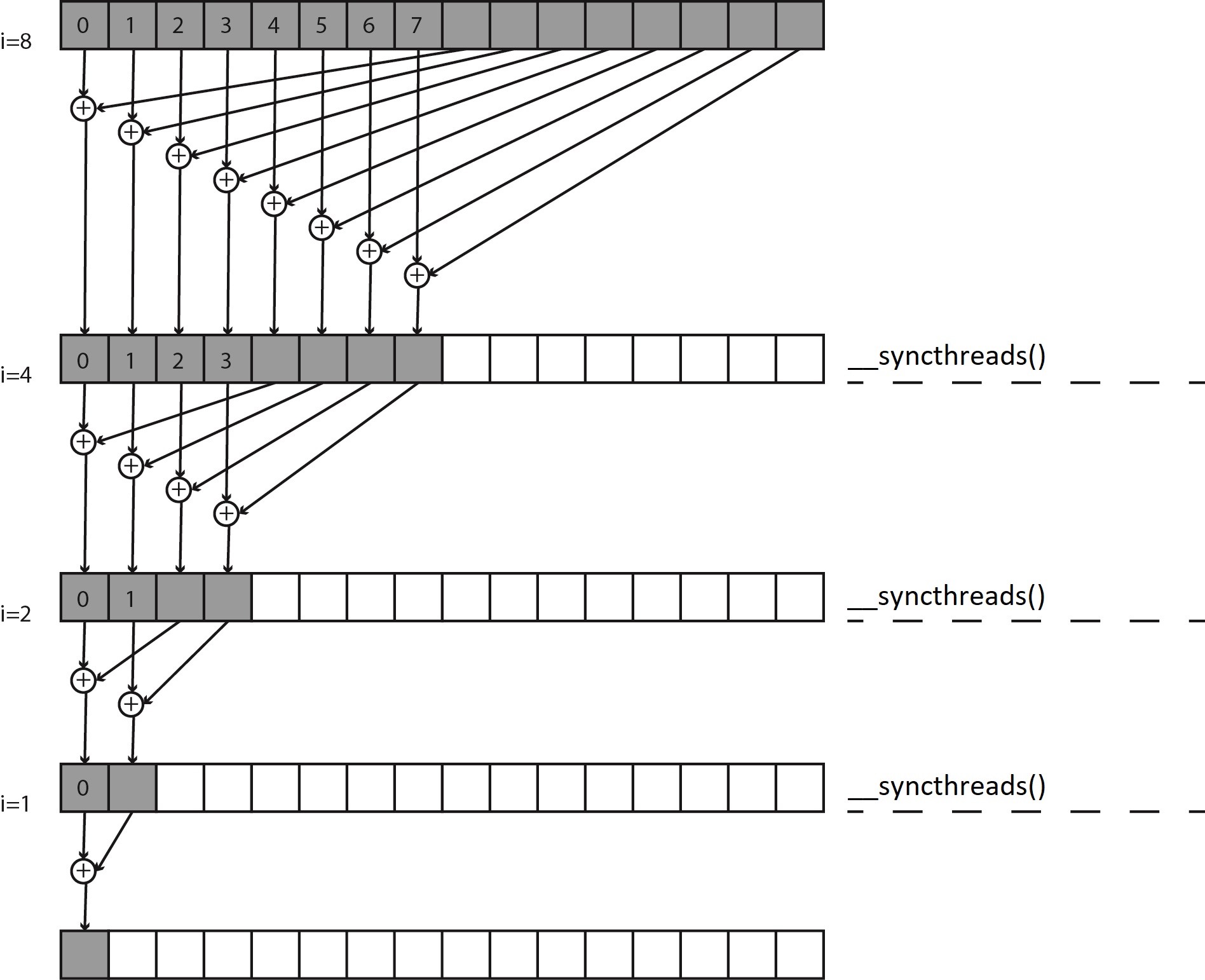
The idea is that each thread adds two values in buf and stores the result back to buf. Since each thread combines two entries into one, we complete the first step with half as many threads as we started with. In the next step, we do the same thing with half of the threads from the first step. We continue until we have the sum of all entries in buf in the first element of buf.

Suppose we have only 16 elements to sum up and 16 threads in a block. In the first step, each of the first eight threads in the block adds the element with index threadIdx.x and the element with indexthreadIdx.x + 8 and writes the sum in the element with index threadIdx.x. Recall that threadIdx.x is the index of a thread within a group. The remaining eight threads from the block do not perform anything. Then all threads wait at the barrier before proceeding with the second step. This is because, in the second step, some of the threads will read the result from the first step. Hence, we have to provide that all threads from the first step have finished writing their result.

In the second step, only the first four threads add the element with index threadIdx.x index and the element with indexthreadIdx.x + 4, while the other threads do not perform anything. Before entering the third step, all threads will again wait at the barrier. Thus, we continue the process until there is only one thread with index 0 left, which will sum up the element with index 0 and the element with index 1. The reduction procedure just described is shown by the code below:

    // Reduction:
    int i = blockDim.x / 2;
    while (i != 0)
    {
        if (threadIdx.x < i)
        {
            // perform the addition:
            buf[threadIdx.x] += buf[threadIdx.x + i];
        }
        i = i / 2;
        // wait at the barrier:
        __syncthreads();
    }

It is important to note that when using a barrier, all threads in the block must execute the barrier function. Suppose the barrier function is called within a conditional statement. In that case, it is important to ensure that all threads in the block enter the conditional statement to execute the barrier. For example, the following code is an illegal use of barrier because all threads will not encounter the barrier:

    if (threadIdx.x < i)
    {
        // perform the addition:
        buf[threadIdx.x] += buf[threadIdx.x + i];
        __syncthreads();
    }      

Any thread with the local index threadIdx.x greater than or equal to i will never execute __syncthreads(). Because of the guarantee that no instruction after a barrier is executed before every thread in the block has reached the barrier, the hardware continues to wait for these threads. This effectively hangs the processor because it results in the GPU waiting for something that will never happen. Such a kernel will actually cause the GPU to stop responding, forcing you to kill your program.

After termination of the while() loop, each block has a single value remaining in the first entry of buf and is the sum of every pair-wise product the threads in that block computed. We should now store this single value in global memory as it will be transferred back to the host. As there is only one element from buf that is written to global memory, only a single thread needs to perform this operation. Since only one thread from each block writes exactly one value to the global array c, we can simply index this entry in c with blockIdx.x, which is the index of the block:

    // only one thread in block writes the result:
    if (threadIdx.x == 0)
    {
        c[blockIdx.x] = buf[0];
    }

The last step of the dot product is to sum the entries of c. Because array c is relatively small, we return control to the host and let the CPU finish the final step of the addition, summing the array c. The following listing shows the entire kernel function for vector dot product using shared memory and summation reduction.

#include <stdio.h>
#include <stdlib.h>

#include <cuda.h>
#include <cuda_runtime.h>

#include "helper_cuda.h"

#define BLOCK_SIZE 64

// CUDA kernel. Each thread takes care of one element of c, each thread block preforms reduction
__global__ void dotProduct(const float *a, const float *b, float *c, int n)
{
    // Get global thread ID
    int tid = blockIdx.x * blockDim.x + threadIdx.x;

    __shared__ float buf[BLOCK_SIZE];

    // Initialize shared buffer
    buf[threadIdx.x] = 0;

    // Make sure we do not go out of bounds
    while (tid < n)
    {
        buf[threadIdx.x] += a[tid] * b[tid];
        tid += gridDim.x * blockDim.x;
    }

    __syncthreads();

    // Reduction:
    int i = blockDim.x / 2;
    while (i != 0)
    {
        if (threadIdx.x < i)
        {
            // perform the addition:
            buf[threadIdx.x] += buf[threadIdx.x + i];
        }
        i = i / 2;
        // wait at the barrier:
        __syncthreads();
    }

    // only one thread in block writes the result:
    if (threadIdx.x == 0)
    {
        c[blockIdx.x] = buf[0];
    }
}

int main(int argc, char *argv[])
{
    // Size of vectors
    int n = 1024;
    dim3 blockSize = BLOCK_SIZE;
    dim3 gridSize = n / blockSize.x;

    size_t datasize = sizeof(float) * n;
    size_t partial_results_size = sizeof(float) * gridSize.x;

    // Host input vectors
    float *h_a;
    float *h_b;
    // Host output vector
    float *h_c;

    // Device input vectors
    float *d_a;
    float *d_b;
    // Device output vector
    float *d_c;

    // Allocate memory for each vector on host
    h_a = (float *)malloc(datasize);
    h_b = (float *)malloc(datasize);
    h_c = (float *)malloc(partial_results_size);

    // Allocate memory for each vector on GPU
    checkCudaErrors(cudaMalloc(&d_a, datasize));
    checkCudaErrors(cudaMalloc(&d_b, datasize));
    checkCudaErrors(cudaMalloc(&d_c, partial_results_size));

    // Initialize vectors on host
    for (int i = 0; i < n; i++)
    {
        h_a[i] = 1.0;
        h_b[i] = 1.0;
    }

    // Copy host vectors to device
    checkCudaErrors(cudaMemcpy(d_a, h_a, datasize, cudaMemcpyHostToDevice));
    checkCudaErrors(cudaMemcpy(d_b, h_b, datasize, cudaMemcpyHostToDevice));

    // Create CUDA events
    cudaEvent_t start, stop;
    cudaEventCreate(&start);
    cudaEventCreate(&stop);

    // Record start event on the stream
    cudaEventRecord(start);

    // Execute the kernel
    dotProduct<<<gridSize, blockSize>>>(d_a, d_b, d_c, n);

    // record stop event on the stream
    cudaEventRecord(stop);
    getLastCudaError("dotProduct() execution failed\n");

    // wait until the stop event completes
    cudaEventSynchronize(stop);    

    // Calculate the elapsed time between two events
    float milliseconds = 0;
    cudaEventElapsedTime(&milliseconds, start, stop);
    printf("Kernel Execution time is: %0.3f milliseconds \n", milliseconds);

    // Copy array back to host
    checkCudaErrors(cudaMemcpy(h_c, d_c, partial_results_size, cudaMemcpyDeviceToHost));

    // Sum up the products
    float result = 0.0;
    for (int i = 0; i < gridSize.x; i++)
        result += h_c[i];
    printf("Result = %.2f \n", result);

    // Release device memory
    checkCudaErrors(cudaFree(d_a));
    checkCudaErrors(cudaFree(d_b));
    checkCudaErrors(cudaFree(d_c));

    // Clean up the two events
    cudaEventDestroy(start);
    cudaEventDestroy(stop);

    // Release host memory
    free(h_a);
    free(h_b);
    free(h_c);

    return 0;
}

The above code is published in folder 05-dot-product-reduction of the workshop's repo.

Measuring Elapsed Time using Events

We have completed the dot product task with two versions of CUDA programs. So how do we determine which version takes less time to finish? This task is actually easy to accomplish using the CUDA events in A streams.

A CUDA stream refers to a sequence of asynchronous CUDA operations that execute on a device in the order issued by the host code. These operations can include host-device data transfer, kernel launches, and most other commands that are issued by the host but handled by the GPU device. The execution of an operation in a stream is always asynchronous with respect to the host. Throughout this course, a typical pattern in CUDA programming has been:

Move input data from the host to the device.
Execute a kernel on the device.
Move the result from the device back to the host.

The data transfers between the host and device using cudaMemcpy() are synchronous (or blocking) transfers. Synchronous data transfers do not begin until all previously issued CUDA calls have been completed. Furthermore, any subsequent CUDA calls cannot begin until the synchronous transfer has been completed (first item). Kernel launches, on the other hand, are asynchronous. Once the kernel is launched (second item), control returns immediately to the CPU and does not wait for the kernel to complete. While this might seem to set up a race condition for the device-to-host data transfer (third item), the blocking nature of the data transfer ensures that the kernel completes before the transfer begins.

An event in CUDA is essentially a GPU time stamp in a CUDA stream that is recorded at a user-specified point in the flow of operations in that stream. The CUDA API provides functions that allow you to insert events at any point in a stream as well as query for event completion. An event recorded on a given stream will only be completed when all preceding operations in the same stream have been completed. The API is relatively easy to use since taking a time stamp consists of just two steps: creating an event and subsequently recording an event.

We can use events to check if the executing stream has reached a given point. You can think of them as operations added to a CUDA stream whose only action when executed from the head of the queue is to raise a host-side flag to indicate completion.

An event is queued to a CUDA stream using the following function:

cudaError_t cudaEventRecord(cudaEvent_t event, cudaStream_t stream = 0);

The passed event can be used to either wait for the completion of all preceding operations in the specified stream. Waiting for an event blocks the calling host thread and is performed using the following function:

cudaError_t cudaEventSynchronize(cudaEvent_t event);

We can measure the elapsed time of CUDA operations marked by two events using the following function:

cudaError_t cudaEventElapsedTime(float* ms, cudaEvent_t start, cudaEvent_t stop);

This function returns the time elapsed between the events start and stop in milliseconds.

The following code sample illustrates how events are used to time device operations:

    // Create CUDA events
    cudaEvent_t start, stop;
    cudaEventCreate(&start);
    cudaEventCreate(&stop);

    // Record start event on the stream
    cudaEventRecord(start);

    // Execute the kernel
    dotProduct<<<gridSize, blockSize>>>(d_a, d_b, d_c, iNumElements);

    // Record stop event on the stream
    cudaEventRecord(stop);
    getLastCudaError("dotProduct() execution failed\n");

    // Wait until the stop event completes
    cudaEventSynchronize(stop);    

    // Calculate the elapsed time between two events
    float milliseconds = 0;
    cudaEventElapsedTime(&milliseconds, start, stop);
    printf("Kernel Execution time is: %0.3f milliseconds \n", milliseconds);

The above code is published in folder 06-dot-product-reduction-profile of the workshop's repo.

© Patricio Bulić, University of Ljubljana, Faculty of Computer and Information Science. The material is published under license CC BY-NC-SA 4.0. ↩

Dot product1