Optimising kernel code

In the previous section, we adjusted the memory interfaces to optimize data transfers between the kernel and global memory. Now, we turn our attention to the kernel's datapath. To achieve this, we introduce pragma directives and observe their impact on the synthesized kernel's latency. This time, we employ Vitis HLS as we focus solely on the results of kernel synthesis, disregarding the overall application. To simplify the HLS flow, we have written a simple tcl script that automates the process. The HLS flow initiates with software-level design simulation, followed by hardware synthesis. For simulation validation, a straightforward test bench program has been created to ensure the correctness of our program. The instructions for running the HLS flow are described in the code repository.

We start with the following code:

#include "matv_mult_opt.h"
#define BLOCK_DIM_SIZE 128

void matv_mult_opt(int* c,
    const int* a,
    const int* b){

    #pragma HLS interface m_axi port=a bundle=aximm1 max_read_burst_length = 16 max_write_burst_length = 16
    #pragma HLS interface m_axi port=b bundle=aximm2 max_read_burst_length = 16 max_write_burst_length = 1
    #pragma HLS interface m_axi port=c bundle=aximm1 max_read_burst_length = 16 max_write_burst_length = 16

    //#pragma HLS dataflow
    // max_read_burst_length denotes the number of elements in the burst
    int a_local[BLOCK_DIM_SIZE][BLOCK_DIM_SIZE];  

    int b_local[BLOCK_DIM_SIZE];
    int c_local[BLOCK_DIM_SIZE];

    // load matrix a into local RAM 
    I_load_a:
    for (int i = 0; i < BLOCK_DIM_SIZE; i++) {
        // we use loop_tripcount only for analysis purpose
        // it does not translate to hardware 
        #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
        J_load_a:
        for (int j = 0; j < BLOCK_DIM_SIZE; j++) {
            #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE 
            a_local[i][j] = *(a + (i * BLOCK_DIM_SIZE + j));
        }
    }


    // load vector b into local RAM
    I_load_b:
    for (int i = 0; i < BLOCK_DIM_SIZE; i++) {
        #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
        b_local[i] = *(b + i);
    }


    // compute matrix vector product
    int tmp;
    I_matv:
    for (int i = 0; i < BLOCK_DIM_SIZE; i++) {
        #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
        tmp = 0;            
        J_matv:
        for (int j = 0; j < BLOCK_DIM_SIZE; j++) {
            #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
            tmp += a_local[i][j] * b_local[j];
        }
        c_local[i] = tmp;
    } 

    // store result in global memory
    I_store_c:
    for (int i = 0; i < BLOCK_DIM_SIZE; i++) {
        #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
        *(c + i) = c_local[i];
    }

}

Compared to the previous version, a new pragma directive, HLS loop_tripcount, is introduced. With the HLS loop_tripcount directive, we specify only the maximum number of iterations for given loops, enabling the synthesizer to generate a more accurate latency and resource consumption report. Importantly, this pragma is purely for analysis and does not impact the synthesized designs. Moreover, unlike in the previous version, we fix the dimension of the matrix and vector to 64 in this kernel.

After running the synthesis, we get the following latencies for each synthesized module:

Module	Load_A	Load_B	MatV	Store_C	Overall
Latency	4099	67	259	67	4476

The resulting report yields several key insights:

1. Loops responsible for loading the input matrix and array, as well as storing results, are pipelined. The tool automatically pipelines loops when possible.
2. Loops handling array loading are flattened and designated as perfect loops. In perfect nested loops, loop bounds are constant, and only the innermost loop contains functionality.
3. The report indicates that the loops responsible for matrix-vector multiplication are also pipelined. However, the tool has encountered an Initiation Interval issue. The Initiation Interval represents the number of cycles the next loop needs to wait after the previous loop has entered. This issue arises when the tool struggles to set the Initiation Interval (II) to 1, indicating a challenge in achieving the desired pipeline depth for optimal performance. Resolving Initiation Interval issues requires careful analysis and adjustments to the code or pragma directives to enable the tool to achieve the desired pipeline structure.

Further inspecting the log files, we encounter the following warning:

WARNING: [HLS 200-885] The II Violation in module 'matv_mult_opt_Pipeline_I_loop' (loop 'I_loop'): Unable to schedule 'load' operation ('a_local_load_16', ../src/matv_mult_opt.cpp:57) on array 'a_local' due to limited memory ports (II = 1). Please consider using a memory core with more ports or partitioning the array 'a_local'.

Array partition

To resolve this issue, we will employ array partitioning. By partitioning arrays, the synthesized design is divided into smaller chunks that can be accessed in parallel, eliminating unnecessary waiting time. In the subsequent round of synthesis, we introduce the following pragmas to completely partition arrays on their elements:

#pragma HLS array_partition variable=a_local type=complete
#pragma HLS array_partition variable=b_local type=complete
#pragma HLS array_partition variable=c_local type=complete

After running the synthesis, we get the following latencies for each synthesized module:

Module	Load_A	Load_B	MatV	Store_C	Overall
Latency	4099	67	66	66	4283

The above table and the report indicate that array partitioning has effectively addressed the initiation interval issue. By partitioning the arrays, we have successfully met the data demands for matrix-vector multiplication. This enables the loops to access matrix elements concurrently, a scenario not possible in the previous case where all elements were stored in a single RAM structure.

Let's compare the resource utilization:

Module	LUTs	FF	DSP	BRAM
Base version	6157	4434	48	4
Array Partitoning	47097	139378	192	4

The table above shows that array partitioning has increased LUT and FF utilization, which are now utilized for synthesizing various RAM chunks. Given our kernel's small and simple nature, enforcing complete partitioning is feasible. Alternatively, one can experiment with block or cyclic types of partitioning using various factors, such as 4, to find a suitable balance between resource utilization and performance.

Manual loop partition

To further improve the performance of the kernel, we can manually divide the loop by rewriting the code for matrix-vector multiplication. Specifically, we replace the nested loops I_matv and J_matv with the pair I_matv1, J_matv1, and I_matv2, J_matv2:

I_matv1:
for (int i = 0; i < BLOCK_DIM_SIZE/2; i++) {
    #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE/2
    tmp = 0;            
    J_matv1_loop:
    for (int j = 0; j < BLOCK_DIM_SIZE; j++) {
        #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
        tmp += a_local[i][j] * b_local[j];
    }
    c_local[i] = tmp;
} 

I_matv2:
for (int i =  BLOCK_DIM_SIZE/2; i < BLOCK_DIM_SIZE; i++) {
    #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE/2
    tmp = 0;            
    J_matv2_loop:
    for (int j = 0; j < BLOCK_DIM_SIZE; j++) {
        #pragma HLS loop_tripcount max=BLOCK_DIM_SIZE
        tmp += a_local[i][j] * b_local[j];
    }
    c_local[i] = tmp;
}

Although the modified code may appear redundant at first glance, it positively impacts hardware implementation. The tool synthesizes separate blocks for I_matv1,J_matv1, and I_matv2, J_matv2, allowing parallel processing of these blocks. Analyzing the reports, we observe that both sets of loops require approximately half the cycles compared to the original loops, contributing to an overall reduction in latency. The decrease in cycles leads to increased utilization of FPGA resources. Despite successfully improving latency, it is evident that the loops for loading the matrix remain the most time-consuming part of the kernel. Unfortunately, further improvements in latency are constrained as all reads in the loops communicate with a shared AXI MM adapter. Increasing the number of AXI MM adapters could be considered to achieve better performance. However, we will not pursue further enhancements to the kernel for the current scope. After we synthesized the design, we obtained the following results:

Module	Load_A	Load_B	MatV1	MatV2	Store_C	Overall
Latency	4099	67	34	34	66	4251

The above code is published in folder 04-matv_mult-hls of the workshop's repo.

Dataflow optimization

We optimized the kernel datapath to achieve a lower delay. However, even though the synthesized kernel employs pipelining to boost its performance, it cannot start processing new matrix-vector multiplication until the previous one finishes. To facilitate pipeline execution at the task level, we will employ the dataflow optimization. The dataflow optimization enables task-level pipelining, enhancing the concurrency of functions and loops in their operation. This concurrency boosts the overall throughput of the RTL implementation. While the Vitis HLS tool naturally seeks to minimize latency and improve concurrency, data dependencies can limit these optimizations. For instance, functions or loops accessing arrays must complete all reads and writes before the next operation can start. The dataflow optimization, activated by the DATAFLOW pragma, addresses this limitation by allowing operations in a function or loop to commence before the previous one completes all its operations. When DATAFLOW pragma is specified, the HLS tool analyzes the data flow between sequential functions or loops. It establishes channels (using ping pong RAMs or FIFOs) that enable consumer functions or loops to start operation before the production functions or loops are completed. This parallel operation reduces latency and enhances the RTL throughput. If no initiation interval (the number of cycles between the start of one function or loop and the next) is specified, the HLS tool endeavors to minimize the initiation interval and commence operation as soon as data becomes available.

Before applying dataflow optimization, we restructured the code so that functions replace every set of loops with the same functionality. The kernel code is given as:

void matv_mult_opt(int* c,
    const int* a,
    const int* b){

    #pragma HLS interface m_axi port=a bundle=aximm1 max_read_burst_length = 16 max_write_burst_length = 16
    #pragma HLS interface m_axi port=b bundle=aximm2 max_read_burst_length = 16 max_write_burst_length = 1
    #pragma HLS interface m_axi port=c bundle=aximm1 max_read_burst_length = 16 max_write_burst_length = 16

    #pragma HLS dataflow
    // max_read_burst_length denotes the number of elements in the burst
    int a_local[BLOCK_DIM_SIZE][BLOCK_DIM_SIZE];  

    int b_local[BLOCK_DIM_SIZE];
    int c_local[BLOCK_DIM_SIZE];

    #pragma HLS array_partition variable=a_local type=complete
    #pragma HLS array_partition variable=b_local type=complete
    #pragma HLS array_partition variable=c_local type=complete

    // load matrix a into local RAM 
    load_matA(&a_local[0][0], a);

    // load vector b into local RAM
    load_vecB(b_local, b);

    // compute matrix vector product
    mat_mult(c_local, &a_local[0][0], b_local);

    // store result in global memory
    store_result(c, c_local);
}

After synthesizing the kernel, we review the log files once again. The latency remains the same compared to the previous kernel version, but we observe a change in the initiation interval. We can summarize the obtained results as follows:

Module	Latency	Interval
Base version	4476	4476
Array Partitoning	4251	4251
Dataflow	4283	4108

In the last case, the interval was equal to the latency of the kernel, indicating that a new operation cannot start until the previous one finishes. The interval is smaller than the kernel delay, allowing a subsequent matrix-vector multiplication to begin before the previous one is finished. Upon closer inspection of the report, we find that the interval is equal to the latency of the part for loading matrix A. Consequently, no new matrix-vector multiplication can start until the previous loading of matrix A and vector B is complete. In Vitis, we can utilize the Dataflow viewer to illustrate the datapath of the synthesized kernel.

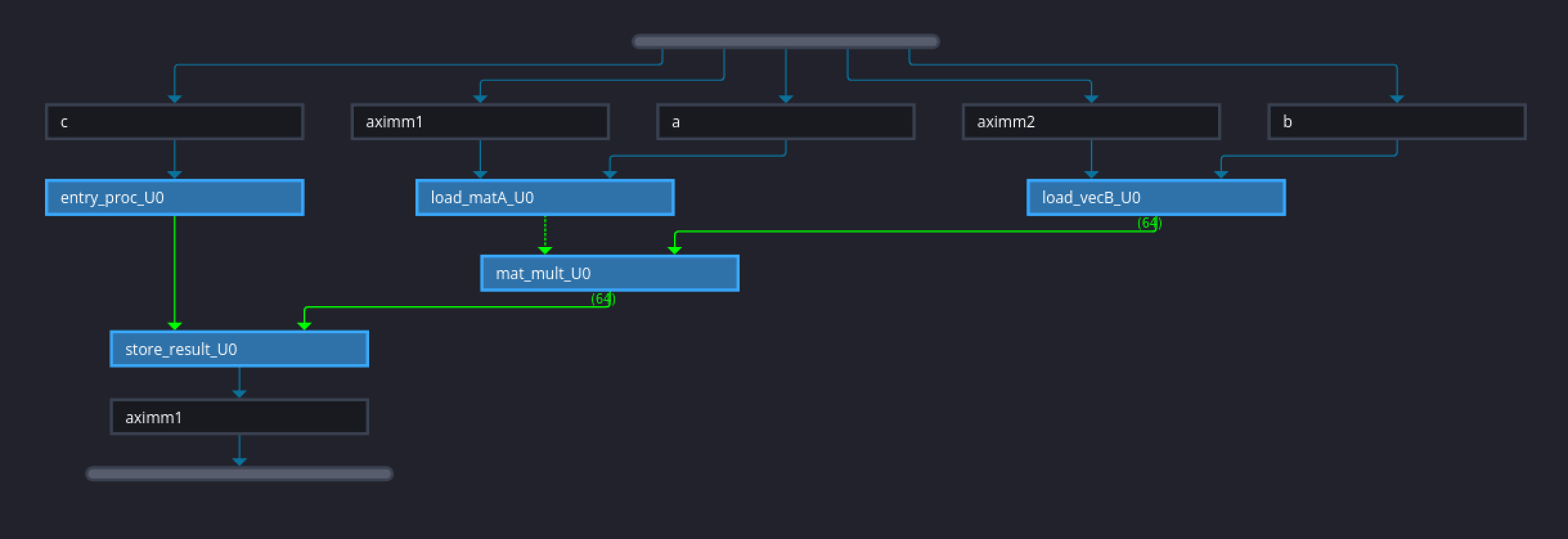
For the complete code, refer to the following link.

---

1. © Nejc Ilc and Ratko Pilipović, University of Ljubljana, Faculty of Computer and Information Science. The material is published under license CC BY-NC-SA 4.0. ↩